Улучшение алгоритма: взвешивание и сжатие

Мы рассмотрели алгоритмы быстрого объединения и поиска. Оба просты в реализации, но не могут поддерживать большие задачи динамической связности. Как сделать их лучше? Рассмотрим этот вопрос. Одно из улучшений называется взвешиванием.

Идея в том, чтобы при реализации быстрого объединения избежать высоких деревьев. Есть большое и малое дерево для объединения, постарайтесь не помещать большое дерево ниже, чтобы не получить высокое дерево. Для этого есть относительно простой способ. Будем отслеживать количество объектов в каждом дереве и следить за тем, чтобы корень малого дерева был соединен с корнем большого дерева.

Таким образом можно избежать ситуации, при которой высокое дерево оказывается внизу. Во взвешенном алгоритме мы всегда ставим меньшее дерево ниже. Посмотрим на реализацию. Начинаем со стартовой позиции, когда каждый в своем собственном дереве. Когда нужно объединить только 2 элемента, то всё работает как обычно. Но если мы объединяем 8 с 4 и 3, то делаем 8 наследником независимо от порядка аргументов, потому что это меньше дерево. 6 и 5: не важно какое дерево идет ниже. 9 и 4: сейчас 9 — это меньшее дерево, 4 — большее. Тогда 9 становится ниже. 2 и 1, 5 и 0. 5 — большее дерево, тогда 0 идет вниз. 7 и 2, 2 — большее дерево, тогда 7 идет ниже. 6 и 1 находятся в деревьях одного размера. 7 и 3: 3 в меньшем дереве т.е. становится ниже.



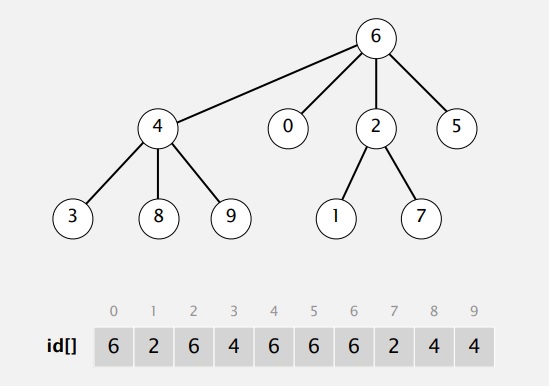
Взвешенный алгоритм гарантирует, что меньшее дерево будет ниже. И снова мы получили одно дерево со всеми объектами. Но в этот раз есть гарантия, что ни один объект не будет слишком далеко от корня. Вот пример взвешенного быстрого объединения, в котором мы всегда помещаем меньшее дерево вниз.



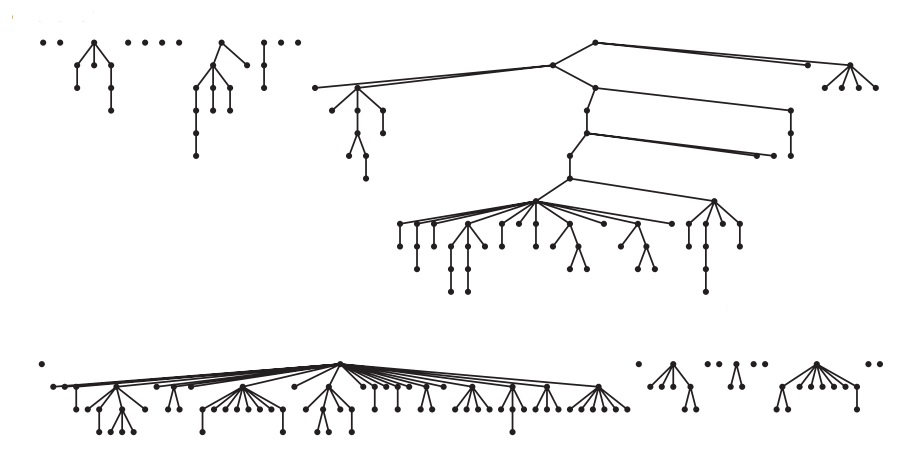
Здесь 100 объектов и 88 операций объединения. Вверху мы видим большое дерево, имеющее некоторые узлы далеко от корня. Внизу все узлы находятся на расстоянии 4 или менее. Среднее расстояние к корню намного меньше.

Теперь посмотрим на Java реализацию, а затем рассмотрим более детально количественные показатели. Мы использовали ту же структуру данных, но в этот раз нам нужен дополнительный массив, содержащий для каждого элемента количество объектов его дерева. Это пригодится для операции объединения. Операция поиска идентична быстрому поиску — вы просто проверяете равны ли корни.

return root(p) == root(q);

Для реализации объединения изменим код для проверки размера. Соединим корень меньшего дерева с корнем большего в каждом случае. После изменения id мы также меняем массив размеров. Устанавливаем i наследником j и увеличиваем размер дерева j на размер дерева i. Или наоборот — увеличиваем размер дерева i на размер дерева j.

int i = root(p);
int j = root(q);
if (i == j) return;
if (sz[i] < sz[j]) {id[i] = j; sz[j] += sz[i];}
else { id[j] = i; sz[i] += sz[j]; }

Последние три строчки – это код для реализации быстрого объединения. Немного кода, но гораздо лучшая производительность. Можно проанализировать время работы математически.

Описанная операция занимает время пропорциональное расстоянию от узла до корня дерева, но можем показать, что максимальная "глубина" любого узла в дереве не превышает логарифма по основанию 2 от N. Обозначение Lg используем для логарифма по основанию 2. Для N = 1000, lg равен 10, для миллиона — 20. Для миллиарда —30. Очень маленькие числа по сравнению c N.

Так как глубина любого узла x не более чем lg(N), это сильно влияет на производительность алгоритма. Инициализация всегда занимает время, пропорциональное N. Но теперь и объединение и поиск занимают время, пропорциональное логарифму от N по основанию 2. И такой алгоритм масштабируется. Если N вырастает с миллиона до миллиарда, то затраты увеличиваются с 20 до 30, что достаточно приемлемо.

На этом можно было бы остановиться, но как обычно происходит при разработке алгоритмов, теперь мы понимаем, за счет чего можно улучшить производительность, и стараемся ещё улучшить алгоритм. В данном случае это легко сделать. Воспользуемся идеей уплотнения пути. Пока мы пытаемся найти корень дерева, содержащего заданный узел, мы проходим все узлы на пути от заданного до корня. Мы можем все их связать с корнем: ищем корень P, а после этого проходим обратно и указываем каждому узлу на корень. От этого будут дополнительные затраты. Мы прошли по пути, чтобы найти корень. Теперь пройдем снова, чтобы сжать дерево. Всего лишь с помощью одной строки кода. Чтобы написать такой код, используем простой вариант с присвоением каждому узлу наследования. Это не так хорошо, как полное сжатие, но тоже хорошо.

private int root(int i)
{
 while (i != id[i])
 {
 id[i] = id[id[i]];
 i = id[i];
 }
 return i;
}

Одной строкой кода можем сделать наше дерево практически полностью плоским. Этот алгоритм был открыт довольно давно, после открытия взвешенности, он оказался весьма интересным для анализа.

Благодаря взвешенному алгоритму быстрого объединения со сжатием пути можно решать задачи, не имеющие других решений. Я приводил пример с миллиардом операций и объектов, что могло бы занять 30 лет. Мы можем решить задачу за 6 секунд. Важно понимать, что именно алгоритм помогает в решении задачи. Быстрый компьютер не при чем. Можно потратить миллионы на суперкомпьютер и сократить время решения с 30 лет до 6 или даже до 2 месяцев. А благодаря алгоритму всё решается за секунды на домашнем ПК.