Алгоритм быстрого объединения

Алгоритм быстрого поиска, который мы рассматривали в предыдущей статье, не подходит для крупных задач в связи с низкой скоростью работы. Что же делать? Давайте попробуем его модернизировать с помощью быстрого объединения. Мы используем так называемый "ленивый подход" к дизайну алгоритмов, при котором стараемся избежать работы, если это возможно.

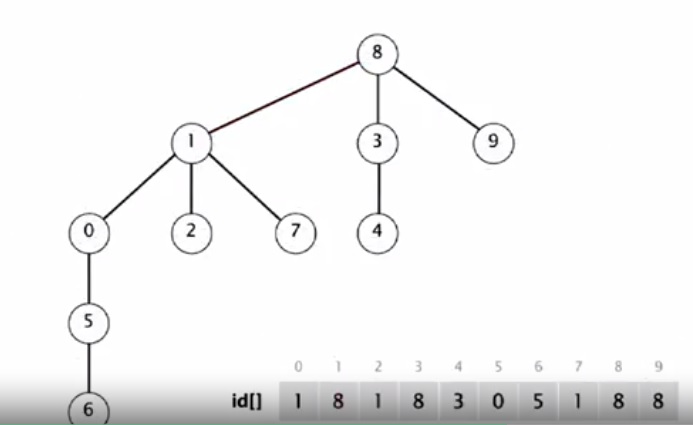
Алгоритм использует ту же структуру данных (массив id[] размера M), но теперь в нем содержатся другие данные. Будем рассматривать этот массив как множество деревьев. Каждый элемент массива будет содержать ссылку на родителя в этом дереве. К примеру, у 3 родитель — 4, у 4 родитель — 9. Поэтому 3-м элементом массива будет 4.



Каждый элемент массива теперь связан с корнем своего дерева. Элементы, расположенные отдельно, связаны сами с собой и указывают на себя. Так, 1 указывает на себя, но и 9 указывает на себя. Это корень дерева, содержащего 2, 4 и 3. Такая структура данных позволяет связать каждый элемент с корнем.

Как только мы сможем вычислять эти корни, то сможем и реализовать операцию поиска (find) просто проверяя, имеют ли проверяемые два элемента один и тот же корень. Этот вопрос эквивалентен вопросу, принадлежат ли они одной связной компоненте.

Поиск корня каждого элемента потребует работы, но операция объединения (union) очень проста. Чтобы объединить компоненты, содержащие два различных элемента, нужно лишь установить id корня элемента P равным id корня элемента Q.



Например, мы могли бы изменить 9й элемент на 6, чтобы объединить компоненты содержащие 3 и 5. Изменяя одно значение в массиве, объединяем две большие компоненты в одну. Это алгоритм быстрого объединения: операция объединения включает изменение только одного элемента массива. Операция поиска требует немного больше работы. Рассмотрим сперва операцию объединения.

Мы снова начинаем с того же, но сейчас каждый элемент массива представляет собой маленькое дерево с одним узлом, указывающим на себя. Сейчас мы должны объединить 4 и 3 в одну компоненту, взять корень компоненты, содержащей первый элемент и сделать его наследником корня компоненты, содержащей второй элемент. В это случае мы просто делаем 3 родителем 4. Берем первый элемент и делаем его наследником корня компоненты, содержащей второй элемент. Теперь 3,4 и 8 в одной компоненте.

6 становится под 5. 4 — это корень дерева, содержащего 4 и 8. А корень дерева, содержащего 9, — 9. Делаем 9 наследником 8. 2 и 1: здесь легко. Теперь если мы хотим узнать соединены ли 8 и 9, мы просто проверяем имеют ли они тот же корень. У них корень один и тот же, значит они соединены. Корень 4 — 8. Корень 5 — 5. Они различны. Объекты не соединены. 5 и 0. 5 становится наследником 0. 7 и 2: 7 становится наследником корня 2 — 1. 6 и 1: корень 6 это 0, 0 становится наследником 1. Каждая из эти операций объединения состоит из изменения только одного элемента массива. Наконец, 7 и 3. Корень 7 — 1, корень 3 — 8. 1 становится наследником 8. Имеем одну связную компоненту со всеми объектами.



Теперь посмотрим на код реализации быстрого объединения. Конструктор тот же самый. Создаем массив и задаем каждый элемент своим корнем. Теперь у нас есть частный метод поиска корня по всем родителям, пока не найдем элемент такой, что i = ID[i], а если не равны то движемся вверх в дереве, установив i как ID[i].

public class QuickUnionUF
{
 private int[] id;
 public QuickUnionUF(int N)
 {
 //установим идентификатор каждого объекта для себя
//(N доступ к массиву)
 id = new int[N];
 for (int i = 0; i < N; i++) id[i] = i;
 }
 private int root(int i)
 {
 //проходим родительские указатели, пока не достигнем корня
//(глубина доступа к массиву)
 while (i != id[i]) i = id[i];
 return i;
 }
 public boolean connected(int p, int q)
 {
 //проверяем, имеют ли p и q одинаковый корень
 //(глубина доступа к массивам p и q)
 return root(p) == root(q);
 }
 public void union(int p, int q)
 {
 //изменяем корень р, чтобы указать на корень q
 //(глубина доступа к массивам p и q)
 int i = root(p);
 int j = root(q);
 id[i] = j;
 }
}

Итак начиная с любого узла вы просто следуете по ID до i = ID[i], это значит вы в корне. Этот частный метод мы можем использовать, чтобы реализовать операцию поиска или ассоциации. Вы просто находите корень P и корень Q и проверяете, равны ли они. Тогда операция объединения — это просто поиск двух корней и задание второго корнем первого.

По факту здесь меньше кода, нет цикла for. Есть один цикл wile, о котором стоит немного беспокоиться. Но это быстрая и элегантная реализация для решения задачи динамической связности, называемая быстрым объединением.

Может ли этот код эффективно решать большие задачи? К сожалению, быстрое объединение хоть и быстрее, но ещё слишком медленное. И его медлительность отличается от быстрого поиска: иногда оно может быть быстрым, но не во всех ситуациях.

Недостаток быстрого объединения в том, что деревья могут быть слишком большими. Значит, операция поиска будет слишком затратной. Вы можете подниматься по длинному узкому дереву, каждый объект которого указывает на следующий, и операция поиска для объекта снизу может включать проход по всему дереву. Затраты времени на операцию поиска слишком большие, а таких операций может быть много.
статьи IT, алгоритмы, java, теория программирования