Простая реализация алгоритма быстрого поиска на Java

Давайте рассмотрим реализацию алгоритма решения проблемы динамический связности, называемую быстрым поиском. Это так называемый быстрый алгоритм для решения такой задачи. Структура данных, которую мы будем использовать для алгоритма, — это просто целочисленный массив, проиндексированный объектами.

Будем считать, что два объекта P и Q соединены тогда и только тогда, когда их элементы в массиве одинаковы. Пример такого массива на изображении ниже:



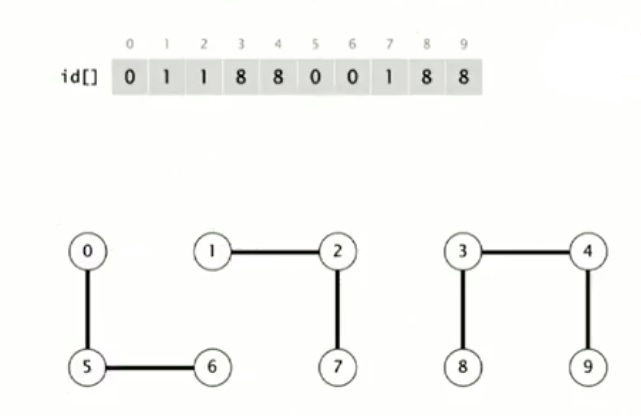
Здесь представлен массив, который описывает ситуацию после 7 соединений. Точки 0, 5 и 6 принадлежат одной компоненте, потому что имеют одинаковое значение в массиве (0). Точки 1, 2 и 7 имеют значение в массиве 1. 3, 4, 8 и 9 - значение 8. Такое представление показывает, что они соединены.

Ясно, что это обеспечит быструю реализацию операции поиска. Мы просто проверяем, равны ли элементы массива. Проверяем, имеют ли P и Q один ID. Так 6 и 1 имеют разные ID. У 1 ID 1, а у 6 — 0. Они не в одной связной компоненте.

А вот объединение сложнее. Для того чтоб объединить компоненты содержащие два данных объекта, мы должны изменить элементы массива, чьи ID равны одному из них на другой. И произвольно мы выбираем изменить те, что равны P на те, что равны Q.

Так если мы объединяем 6 и 1, мы должны изменить элементы 0, 5. и 6. Все из той же связной компоненты, что и 6. От 0 до 1. И это, как мы увидим, проблема, когда имеем дело с большим количеством объектов, потому что много значений могут меняться. Но это легко реализуемо, и это будет нашей стартовой точкой.

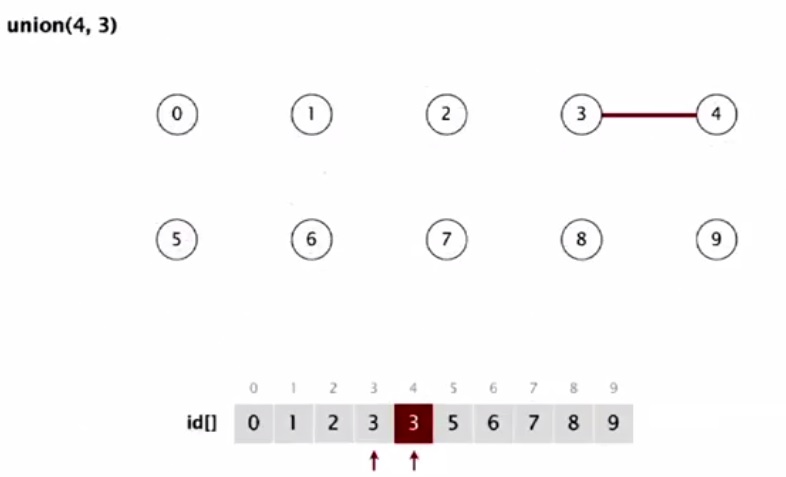
Изначально мы задаем массив ID, где каждый элемент равен его индексу. Можно сказать, что все объекты независимы; они принадлежат собственной связной компоненте. Перейдем к операции объединения. При ней мы должны изменить все элементы, ID которых равны ID первого, на ID второго. Так в этом случае соединения 3 и 4 нам нужно изменить 4 на 3.



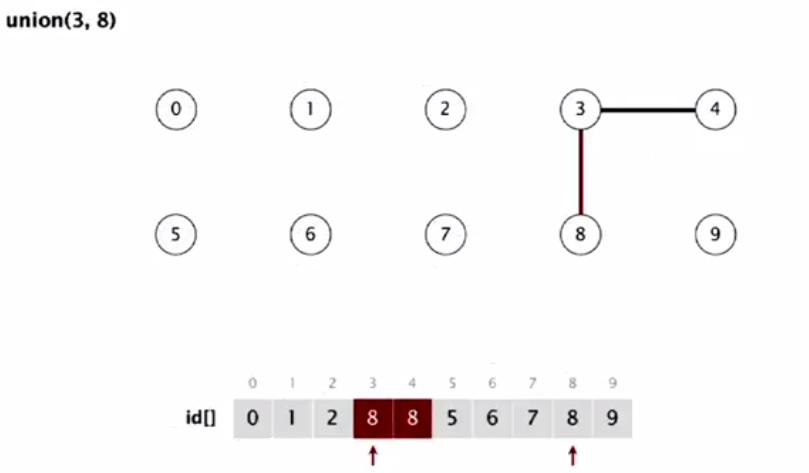
Повторим несколько раз, чтобы вы поняли как это работает. Теперь 3 и 8 должны быть соединены, т.е. сейчас 3 и 4 должны быть соединены с 8. И оба элемента должны измениться на 8.



Это была короткая демонстрация быстрого поиска. Теперь посмотрим на код. После демонстрации несложно перейти к программированию этого алгоритма на Java. Это интересное упражнение на программирование, которое многие могут сделать неверно с первой попытки.

Есть целочисленный массив. Это наш массив ID. Эту структуру данных будем использовать в нашей реализации. Конструктор должен создать массив и затем задать значение соответственно индексу i к i.

public class QuickFindUF {
private int[] id;
public QuickFindUF(int N) {
id = new int[N];
for (int i = 0; i < N; i++) id[i] = i;
}
//connected

//union
}

Операция поиска или проверки связности тоже довольно проста:

public boolean connected(int p, int q) {
return id[p] == id[q];
}

Она просто принимает два аргумента P и Q, проверяет, равны ли их ID, и выводит значение. Если равны, то выводится true, если не равны - false. Более сложная реализация у операции объединения:

public void union(int p, int q)
 {
 int pid = id[p];
 int qid = id[q];
 for (int i = 0; i < id.length; i++)
 if (id[i] == pid) id[i] = qid;
 }

В этом случае мы сначала находим ID, соответствующий первому аргументу, затем ID, соответствующий второму аргументу. А затем проходим весь массив в поиске элементов, чьи ID равны ID первого аргумента и приравниваем их к ID второго аргумента. Это довольно простая реализация.

Это хорошая, наглядная реализация быстрого поиска. Нужно выяснить, насколько эффективным будет этот алгоритм. Важно оценить количество обращений к массиву в программе. В нашей реализации операция инициализации и объединения включали for-цикл по всем элементам массива.

Операция поиска быстрее, она лишь проверяет элементы массива. Проблема в том, что операция объединения слишком затратная. В частности если произвести N операций объединения на N объектах, независимо от того, соединены они или нет, то время будет расти в квадрате, а квадратичное время слишком медленно. Мы не можем использовать алгоритмы с квадратичным временем для больших задач. Они не масштабируются.

При ускорении работы компьютеров квадратичные алгоритмы фактически замедляются. Вот что я имею ввиду: в настоящее время есть компьютеры, которые могут делать миллиарды операций в секунду с миллиардами обращений к памяти. Значит, можно считать всю память за секунду. Удивительно, что такой стандарт актуален уже 50-60 лет. Компьютеры становятся больше и быстрее, чтобы доступ ко всей памяти занимал несколько секунд. Это соблюдалось для компьютеров с тысячью ячейками памяти, соблюдается и сейчас при миллиарде.

Значит, с большим объемом памяти мы можем решить большие задачи. Если иметь миллиард объектов, над которыми мы хотим провести миллиард операций объединения, то такая задача с алгоритмом быстрого поиска может занять 10^18 операций. Если посчитать, то получится около 30 лет вычислений на компьютере. Не практично решать такую задачу на современном компьютере.

Причина в том, что квадратичные алгоритмы не масштабируются вместе с технологиями. На компьютере, который в 10 раз быстрее, можно решить задачу в 10 раз больше. Но если это квадратичный алгоритм, то выйдет в 10 раз медленнее! Таких ситуаций необходимо избегать, разрабатывая более эффективные алгоритмы решения подобных задач. Чем мы и займемся в следующих статьях.
статьи IT, алгоритмы, java, теория программирования