Основы Big O нотации

Big O нотация - это запись в математических выражениях, которая может быть применена к алгоритмам для описания их вычислительной сложности. Она дает возможность получать масштабируемость алгоритма по мере увеличения количества элементов во входных данных, которые он обрабатывает.

Что такое Big O нотация?

Big O notation - это математическая запись, которая может быть применена к алгоритмам, которые мы используем при разработке программного обеспечения. В этом контексте его целью является описание вычислительной сложности алгоритма. В частности, он позволяет оценить, насколько масштабируемым будет алгоритм по мере роста объема обрабатываемых данных. Масштабируемость, указанная нотацией big O, может использоваться для описания различных вещей, таких как время или циклы обработки, необходимые для расширения набора данных, или увеличение использования памяти или ресурсов.

Big O принадлежит к семейству так называемых асимптотических обозначений. Это включает в себя ряд различных обозначений, каждый с другой целью. Цель нотации Big O - указать верхнюю границу или наихудший сценарий для скорости роста алгоритма. Это не точная мера производительности или использования ресурсов. Например, рассмотрим алгоритм, который предлагает Big O notation, имеет линейный рост времени обработки. Удвоение размера набора данных не обязательно означает, что время работы алгоритма удвоится. Это просто означает, что время обработки верхней границы для большего набора данных будет в два раза больше, чем в худшем случае для меньшего ввода.

Нотация

В нотации Big O используется заглавная буква "O", за которой следует функция в круглых скобках. Это функция, которая описывает масштабируемость. Функция почти всегда включает в себя букву "n", которая представляет собой количество элементов в обрабатываемых данных. В следующих подразделах описываются некоторые из наиболее часто встречающихся примеров.

O(1)

O(1) алгоритмы - это те, которые не имеют увеличения сложности, связанной с размером входных данных; время обработки, использование памяти или другой измеряемый элемент фиксированы. Простым примером может служить интегрированный в язык запрос (LINQ), оператор "First". Он возвращает первый элемент из последовательности. Наличие большей последовательности не увеличивает время, необходимое для извлечения первого элемента.

O(log n)

O(log n) описывает алгоритмы с логарифмической масштабируемостью. Они увеличиваются в сложности по мере увеличения количества элементов в наборе данных, но на относительно меньшую величину по мере увеличения размера. Простой пример - алгоритм бинарного поиска для отсортированной последовательности. Каждая итерация этого алгоритма может игнорировать половину оставшихся деталей. Удвоение размера данных поиска добавляет только одну дополнительную итерацию к худшему сценарию поиска.

O(n)

O(n) алгоритмы показывают линейный рост. Простой пример - поиск по несортированному набору данных путем чтения одного элемента за другим, пока не будет найден определенный элемент. В худшем случае, когда искомый элемент является последним в наборе. Добавление дополнительного элемента добавляет одну дополнительную потенциальную итерацию поиска. Этот пример подчеркивает идею о том, что Big O описывает только верхнюю границу. Набор из тысячи или миллиона элементов можно найти за одну итерацию, если элемент, который вы ищете, является первым в списке.

O(n log n)

O(n log n) алгоритмы известны как логлинейные. Часто это алгоритмы, которые могут выполнять операцию O(log n) для каждого элемента входных данных. Несколько алгоритмов сортировки, таких как быстрая сортировка и сортировка кучи имеют сложность O(n log n).

O(n^x)

O(n²), или квадратичные, алгоритмы увеличивают сложность пропорционально квадрату числа элементов во входных данных. Если у вас есть два вложенных цикла для входных данных в вашем алгоритме, например, с пузырьковой сортировкой, это, вероятно, будет O(n²). Другие варианты этого - O(n^x) или полиномиальные алгоритмы. Например, три вложенных цикла будут O(n³), четыре вложенных цикла - O (n⁴) и так далее.

О(хⁿ)

O (2ⁿ) алгоритмы дают экспоненциальный рост и очень плохую масштабируемость. Каждый дополнительный элемент входных данных может удвоить количество времени или ресурсов, используемых алгоритмом. Постоянное значение 2 может быть изменено для алгоритмов с еще более низкой масштабируемостью. Например, O(3ⁿ) указывает, что сложность может утроиться с каждым дополнительным элементом.

О(n!)

Алгоритмы, которые могут рассматривать каждую перестановку элементов в наборе входных данных, являются O(n!), давая факторный рост сложности. Примером такой масштабируемости является попытка решить задачу коммивояжера грубой силой.

Сравнение

По мере продвижения вниз по списку выше масштабируемость становится все хуже с каждым шагом. Чтобы увидеть разницу, рассмотрим следующий график. Это показывает относительный сценарий верхней границы для алгоритмов каждого типа, показывая количество циклов или потребности в ресурсах для каждого типа алгоритма в соответствии с размером входных данных.



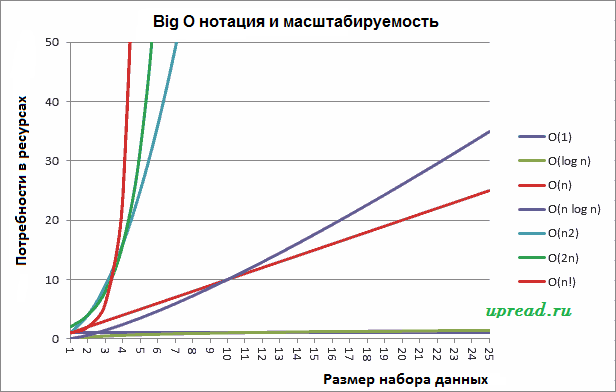
Заключение

При рассмотрении масштабируемости алгоритма для определения правильного варианта big O следует игнорировать константы. Например, представьте, что у вас есть линейный алгоритм, где каждая итерация занимает одну секунду для выполнения. Это O (n). Если вы улучшите код и уменьшите вдвое циклы обработки, необходимые для каждой итерации, вы не будете считать это O(0.5 n). Алгоритм по-прежнему O(n), хотя он работает быстрее.

При вычислении формулы для наихудшего плана выполнения для вашего алгоритма он часто не будет соответствовать одному из вышеупомянутых вариантов. В этих случаях в качестве функции используется только самый бедный элемент масштабируемости. Например, у вас может быть алгоритм, который включает в себя три вложенных цикла, за которыми следуют два вложенных цикла. Наихудший сценарий для количества итераций будет (n³ + n²). Однако, поскольку n³ является более низкой масштабируемостью, вы бы сказали, что алгоритм был O(n³).
статьи IT, алгоритмы, теория программирования