Анализ алгоритмов: введение

Нам необходимо знать основы для понимания работы алгоритмов, чтобы должным образом применять их на практике. В этой серии статей мы будем говорить, о том, как узнать характеристики производительности алгоритмов. Посмотрим, как построить математическую модель алгоритма, а также как классифицировать алгоритмы относительно роста времени их выполнения. Немного поговорим о теории алгоритмов, а также об анализе количества используемой памяти.

Мы обсудим данные проблемы с точки зрения различных персонажей. Первый из них - программист, которому требуется найти решение и заставить его работать. Второй - клиент, который воспользуется любой программой, чтобы завершить работу. Третий — теоретик, который хочет понять, как все на самом деле работает. Наконец, команда с базовыми фундаментальными знаниями, которые бывают необходимы для всей остальной работы. И понемногу будет от каждого в сегодняшней статье. Во время обучения вам нужно быть готовым однажды сыграть одну из этих ролей или даже их все. Очень важно понимать различные точки зрения.

Ключевой момент на котором мы сфокусируемся - время выполнения. На самом деле идея понимания времени выполнения вычислений уходит во времени к Бэббиджу и вероятно даже ранее. И вот цитата Бэббиджа «Как только появится аналитическая машина, она непременно задаст будущее развитие науки. Какой бы результат не искали с ее помощью, возникнет вопрос как организовать вычисления, чтобы получить результат за кратчайшие сроки.»



Если вы посмотрите на машину Бэббиджа, называемую аналитической, у нее есть рычаг. И Бэббиджа очень волновало, как долго будет производиться вычисление, то есть сколько раз нужно повернуть рычаг. И это не сильно отличается от того, что есть сегодня. Рычагом может быть что-то электронное, переключающееся миллиард раз в секунду. Но все так же мы ищем, как много раз некоторая операция должна быть произведена для того, чтобы вычисление было завершено. Есть много причин анализировать алгоритмы.

Мы заинтересованы в предсказании производительности и хотим сравнить производительность различных алгоритмов при решении одной и той же задачи и быть способными предоставить некоторые гарантии того, как они будут выполняться. Это понимание некоторых теоретических основ того, как алгоритмы выполняются.

Но в первую очередь, необходимость анализировать алгоритмы и понимать их обусловлена желанием избежать низкой производительности. Мы хотим быть уверены, что наши алгоритмы завершат работу за то время, что мы ожидаем. Очень часто можно видеть в сегодняшних вычислениях, что клиент получает плохую производительность, потому что программист не понял производительные характеристики алгоритма. Наша цель - сфокусироваться на возможности предсказания производительности и сравнении алгоритмов.

Существует много успешных примеров разработки алгоритмов с лучшей производительностью, позволяющих решать задачи, которые иначе не могли быть решены. Я просто приведу пару примеров. Один из первых и наиболее известных — алгоритм БПФ. Этот алгоритм для разбиения волны от n источников сигнала в периодические компоненты. И это основа для DVD и JPEG и многих других форматов.

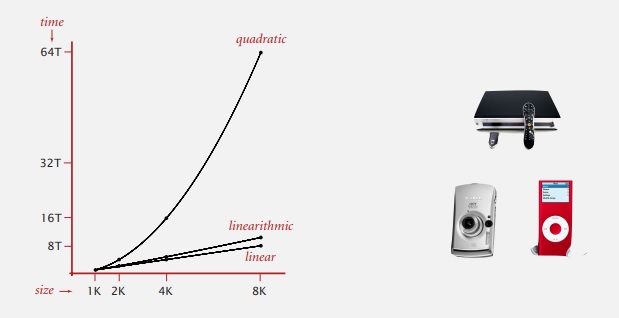
Есть простой способ решения, который занимает время пропорциональное N^2. А алгоритм БПФ занимает только N log N шагов. И разница между N log N и N^2 — это разница между возможностью решить огромные задачи и ее отсутствием. Множество цифровых технологий, цифровых медиа технологий, что мы имеет сегодня, возможны благодаря быстрому алгоритму.



Другой пример был разработан Эндрю Аппелом, нынешним главой кафедры компьютерных наук в Принстоне. Он придумал его, когда работал над дипломом. Это алгоритм для моделирования задачи N тел. Простой алгоритм занимает время пропорциональное N^2, но алгоритм Аппеля был N log N алгоритмом, то есть ученые могли делать моделирование N тел для больших значений N, что сделало возможным новые исследования.

Итак задача, которую мы обычно встречаем, это будет ли моя программа решать большие задачи. Программисты сталкиваются с этим все время. Почему моя программа работает так медленно? Почему ей не хватает памяти? И с этим программисты сталкиваются уже долгое время. Кнут предложил использовать научный подход для понимания производительности алгоритмов в 1970 году. Мы не открыли новый секрет Вселенной, но стали использовать научный метод, и относиться к компьютерам, как к чему-то, что может быть изучено и прийти к пониманию того, как наша программа будет исполняться.

Это лишь обзор того, что мы понимаем под научным методом, который был успешным несколько последних сотен лет. Мы будем наблюдать за некоторыми особенностями окружающего мира. В нашем случае за временем работы компьютера. Затем разработаем гипотезу, модель, которая согласовывается с наблюдениями, и будем надеяться, что гипотеза достаточно хороша и позволит сделать предсказания.

Обычно предсказывается время работы для задачи большого размера, или на разных компьютерах. И затем мы проверяем предсказания, делая еще больше наблюдений, до тех пор пока не удостоверимся, что наша модель и наблюдения согласованны. Таким способом можно определить производительность программы.

У научного метода есть некоторые базовые принципы:

1. если вы проводите эксперимент, то ожидается, что другой человек сможет провести такой же эксперимент и получит тот же результат
2. гипотеза должна иметь свойства того, что эксперименты могут показать ее ошибочность. Она должны быть аккуратно составлена, и мы должны обязательно пробовать сделать это.

Будущее мира природы, который мы изучаем, это компьютер, существующий внутри этого мира. Алгоритмы в таком случае от абстракции становятся физическими явлениями, подобно движению электронов в компьютере.
статьи IT, алгоритмы, теория программирования