Очередь в программировании алгоритмов

Сегодня мы кратко рассмотрим реализацию очереди с использованием базовых структур данных. Итак, вот соответствующий API для QueueOfStrings. На самом деле это тот же API, что и для стеков, различие только в именах. Вместо push у нас enqueue, вместо pop у нас dequeue.



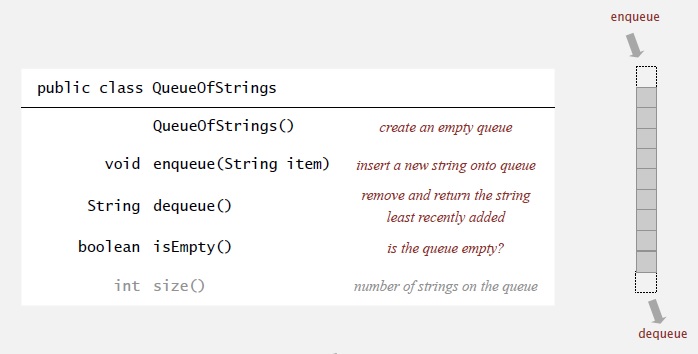
Отличаются они и семантикой. Для enqueue() мы добавляем элемент, допустим, в конец очереди. А для dequeue() удаляем элемент из начала. Это как ждать в очереди, чтобы купить билет. Когда вы встаёте в очередь (enqueue()), то попадаете в конец, а тот, кто простоял дольше всех, выходит из очереди. Посмотрим на реализацию, сначала с помощью связного списка, затем массива. Итак, представление очереди с помощью связного списка.



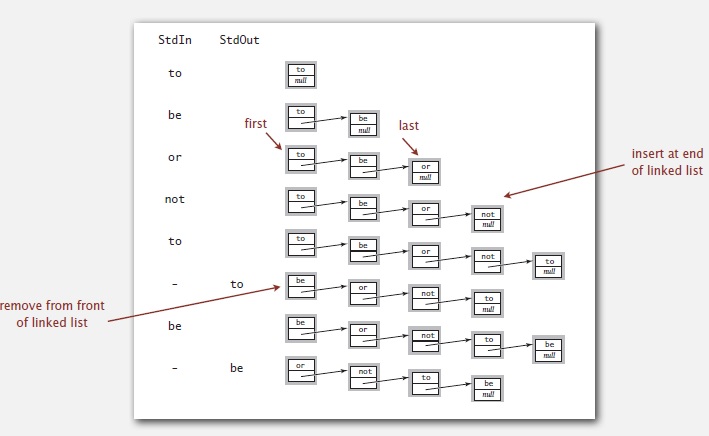
Нам нужно поддерживать два указателя, две ссылки. Одна для первого элемента в списке, а другая — для последнего. Когда мы производим вставку, то добавляем элемент в конец списка, а не в начало. А когда удаляем, то убираем элемент из начала списка. Вот здесь реализация метода dequeue().



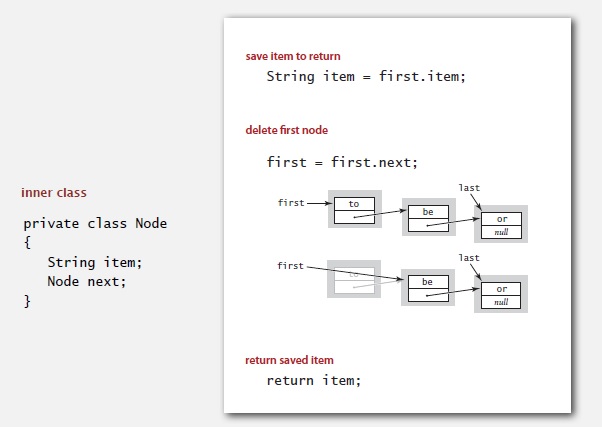
Она идентична коду метода pop() для стека. Сохраняем элемент в переменную, удаляем первый элемент путем замены ссылки на следующий и выводим элемент. Так что код идентичен. При добавлении нового элемента или постановки в очередь: он оказывается последним в очереди. Для добавления его в конец первое что мы делаем — сохраняем ссылку на последний элемент. Нам придется изменить эту ссылку с null на указатель на новый узел. Затем мы создадим новый узел для размещения к конце списка, мы заполним его поля, и затем заменим ссылку с null на ссылку на новый узел. Всего несколько строк кода.

Это основы работы со связными списками. Нам не нужны общие программы для управления связными списками - их инкапсулируют в базовые типы данных подобного рода. Вернемся к нашей полной реализации. Здесь объединенный код:

public class LinkedQueueOfStrings
{
private Node first, last;
private class Node
{ /* StackOfStrings */ }
public boolean isEmpty()
{ return first == null; }
public void enqueue(String item)
{
Node oldlast = last;
last = new Node();
last.item = item;
last.next = null;
if (isEmpty()) first = last;
else oldlast.next = last;
}
public String dequeue()
{
String item = first.item;
first = first.next;
if (isEmpty()) last = null;
return item;
}
}

Мы также учли особые случаи, когда очередь пуста. Если очередь пуста после удаления элемента, то устанавливаем last в null. Обеспечиваем, чтобы first и last были такими, какими нужно. Это детали, которые легко проверить. Что насчет массивов?

Опустим детали, но не трудно реализовать очередь на основе изменяемых массивов. Это несложная, но каверзная задача для программиста — попробуйте сами. У нас 2 указателя: первый элемент очереди и последний, который представляет собой позицию для следующего. При enqueue() новый элемент добавляется в конец списка, а при dequeue() удаляется элемент из начала. Хитрость в том, чтобы при выходе за размер массива переустановить указатель назад в ноль. Отсюда дополнительный код. Также нужно добавить возможность динамического изменения размера для реализации структуры данных такой же, как и для стека. Это задача для вас.
статьи IT, алгоритмы, теория программирования, очередь, java