Анализ алгоритмов: классификация

К счастью, при анализе алгоритмов используется не так много различных функций. Благодаря этому можно классифицировать алгоритмы по их производительности в зависимости от масштабов задачи. Об этом и поговорим.

Хорошая новость в том, что нам нужны всего несколько функций. Конечно, используются и другие, но подавляющее большинство алгоритмов, которые мы рассматриваем, описываются этими несколькими функциями, представленными на графике.



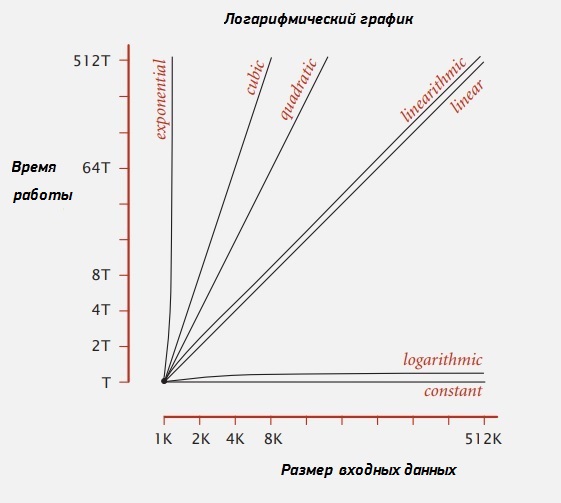
Когда мы говорим о скорости (порядке) роста, то не обсуждаем ведущую константу. Обычно говорим, что время работы алгоритма пропорционально N*Log(N). То есть, мы предполагаем, что время выполнения равно ~C*N*Log(N), где C - некоторая константа.

Эти графики, которые построены в логарифмических координатах, дают хорошее представление о том, что происходит. Если порядок роста логарифмический или константа, не имеет значения, насколько велика задача. Время работы будет небольшим. Если для N=1000 время равно T, то для N=500.000 время по-прежнему близко к T. При линейной зависимости, если порядок роста пропорционален N, тогда по мере роста N время работы увеличивается соответственно. Так же для N*log(N). К подобным алгоритмам мы стремимся. Время работы пропорционально размерам входных данных. Это приемлемая ситуация.

Ранее мы говорили о Union-Find: если график оказывается квадратичным, время работы растет гораздо быстрее, чем размер входных данных. Для больших объемов данных это не подходит. Если зависимость кубическая, то ещё хуже. Нашей главной задачей является определение степени функции.



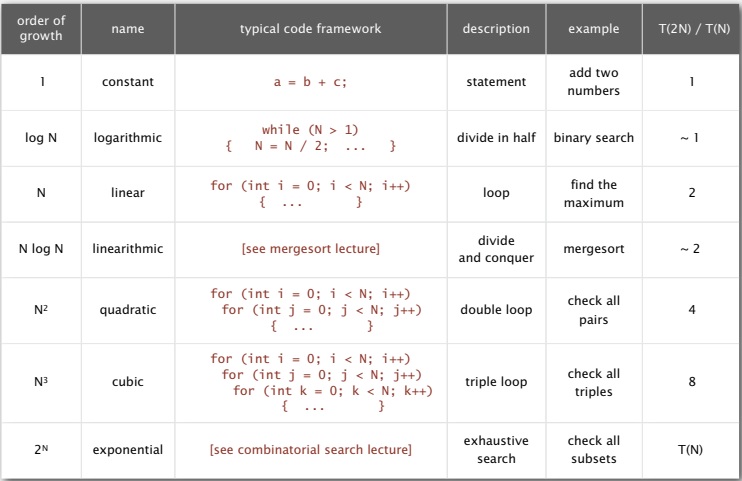
Такая классификация по степени проистекает из кода. Если в коде нет циклов, тогда рост будет линейным. Если в коде есть некий цикл, в котором входные данные делятся пополам, например, алгоритм бинарного поиска, то порядок роста будет логарифмическим. Мы его ещё проанализируем.

Если объем данных удваивается, то время растет линейно. Если вы удваиваете огромный объем данных, то время не растет линейно, а почти не меняется. Изменение в lg(N) раз едва заметно. Если вы перебираете все элементы массива, то время меняется пропорционально N. Типичным примером будет поиск максимума, подсчет числа нулей или задача 1Sum.

Очень интересной категорией является так называемые N*Log(N) алгоритмы или квазилинейные алгоритмы. Для их получения используют специальный принцип "разделяй и властвуй". И алгоритм сортировки слиянием (Mergesort), о котором мы поговорим потом, является главным примером таких алгоритмов.

Если возникает двойной цикл for, как в алгоритме 2-SUM, время работы пропорционально N^2. Как мы видели, оно квадратично. Если тройной цикл for, как в алгоритме 3-SUM, то алгоритм становится кубическим - время работы пропорционально N^3. Для квадратичных или кубических алгоритмов множитель соответственно 4 или 8, т.е. при удвоении N время работы для кубического алгоритма увеличивается в 8 раз. У вас будет время посчитать это, пока ждете завершения работы программы.

Также есть категория алгоритмов, время работы которых экспоненциально, N растет в узких пределах. Сосредоточимся на интересующих нас алгоритмах, а именно тех, что решают задачи больших масштабов — линейных и N*Log(N). Ведь даже на быстрых компьютерах квадратичные алгоритмы могут решать задачи для N=10^4, а кубические алгоритмы — для N=10^3. Они просто не годятся для сегодняшних объемов информации. Этот факт становится всё более очевидным с течением времени.

Можно дискутировать по поводу полезности таких алгоритмов, но ситуация лишь усугубляется. Нужны более быстрые алгоритмы. Проиллюстрируем разработку математической модели, которая описывает производительность алгоритма, на примере алгоритма двоичного поиска. Задача у него такая: есть сортированный массив целых чисел, нужно определить, содержится ли в нем определенный элемент. И если да, то под каким индексом.

Двоичный алгоритм быстро решает эту задачу. Он сравнивает элемент со средним значением. В данном случае, мы ищем 33 и сравниваем его с 53. Если значение меньше, то продолжаем искать в левой половине. Если больше, то поиск надо продолжать в правой половине массива. При равенстве ответ найден. Алгоритм применяется рекурсивно. Посмотрим демонстрацию.

Ищем 33 в массиве. Сравниваем со значением в средней точке массива. Там 53, поэтому остается левая половина массива. Находим значение в середине левой части Это 25. 33 больше, поэтому сдвигаемся вправо. Остается подмассив между 25 и 53. Смотрим в середину - 33 меньше, поэтому мы двигаемся влево. Остался последний элемент, и это 33. Его индекс в массиве - 4. Если ищем элемент, которого нет, то процесс повторяется. Скажем, мы ищем 34. Действия те же. Проверяем левую половину, затем направо. Левее от 43. Остался последний элемент, и это не 34. Значит элемент не в массиве. Вот код двоичного поиска.

Хотя двоичный поиск — простой алгоритм, весьма непросто написать код правильно. Насколько я знаю, правильный код был написан только в 1962 г. А в 2006 году была обнаружена ошибка реализации двоичного поиска в Java. Лишнее напоминание о том, насколько внимательно надо подходить к алгоритмам, особенно для библиотек, которые будут использоваться миллионами людей. Вот реализация.

public static int binarySearch(int[] a, int key)
 {
 int lo = 0, hi = a.length-1;
 while (lo <= hi)
 {
 int mid = lo + (hi - lo) / 2;
 if (key < a[mid]) hi = mid - 1;
 else if (key > a[mid]) lo = mid + 1;
 else return mid;
 }
 return -1;
 }

Она не рекурсивная, хотя можно реализовать и рекурсивную. Она просто отражает в коде то, что я описывал словами. Ищем, находится ли ключ в массиве. Мы используем два указателя - нижний и верхний, для указания интересующей нас части массива. Пока нижний указатель меньше или равен верхнему, мы вычисляем середину. Сравниваем ключ со значением в середине. Если они равны, выводим индекс средней точки. Если меньше - переустанавливаем верхний указатель. Если больше - переустанавливаем нижний указатель. До тех пор, пока они не сравняются. И если они равны, а мы не нашли ключ, то выводим "-1".

Легко убедиться, что эта программа работает как заявлено, размышляя над этим инвариантом. Если ключ в массиве, то он между нижним и верхним указателем.

a[lo] ≤ key ≤ a[hi].

статьи IT, алгоритмы, теория программирования, java