Анализ алгоритмов: математические модели

Наблюдения за происходящим позволяет предсказывать производительность, но не помогает понять работу алгоритма. Разберем математическую модель, чтобы понять суть происходящего.

Эта концепция была разработана и популяризирована Дональдом Кнутом в конце 60-х. В то время компьютерные системы стали действительно сложными, и специалисты в области компьютерных технологий были озабочены тем, смогут ли они понять, что происходит. Кнут не сомневался, что этого можно добиться.

Можно вычислить общее время работы программы путем определения всех базовых операций, затрат на их выполнение, периодичности выполнения и умножения всех затрат на периодичность. Проанализируйте программу для определения набора базовых операций и времени их выполнения в зависимости от компьютера, как мы говорили ранее. Нужно обратиться к математике, т.к. повторяемость зависит от алгоритма и входных данных.

Кнут написал серию книг, которая дает подробный и точный анализ в рамках конкретной компьютерной модели для широкого круга алгоритмов. Таким образом, от Кнута, мы знаем, что в принципе, можно получить точные математические модели производительности алгоритмов или программ. Хорошо. Как же выглядит этот процесс?

Если хотите, можете проводить эксперименты. В былые времена мы воспользовались бы руководством. Каждый компьютер снабжался руководством, в котором было точное время выполнения каждой инструкции. Сейчас с этим сложнее, поэтому мы проводим эксперименты.



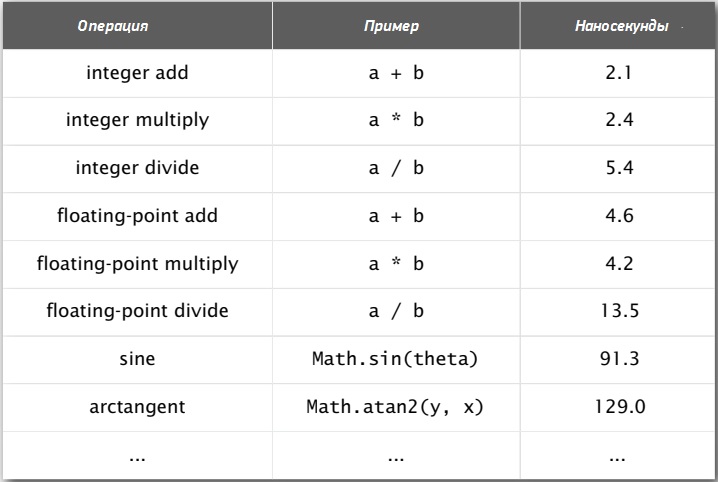
Можно провести миллиард действий сложения и обнаружить, что компьютер затрачивает на сложение 2,1 наносекунду. Можно выполнить более сложные функции, вроде вычисления синуса или арктангенса, это подводит нас к анализу алгоритмов. То есть способы определения временных затрат существуют.

В большинстве случаев мы принимаем эти затраты за константу и можем вычислить её значение. Правда, когда мы работаем с набором из N объектов, есть операции, которые занимают время, пропорциональное N. Так, например, если вы выделяете память для массива размером N, это занимает время пропорциональное N, потому что в Java по умолчанию всем элементам массива присваиваются нулевые значения. В других операциях всё зависит от системной реализации.

Важным случаем является соединение строк. Если вы соединяете две строки, время работы пропорционально длине строки. Начинающие программисты ошибаются, считая, что эта операция фиксированного времени выполнения. А она такой не является. Это временные затраты на операции. Более интересна повторяемость их выполнения.

Вот очень простой вариант 3-SUM задачи - задача 1-SUM, которая заключается в определении того, сколько чисел при сложении дают 0.

int count = 0;
for (int i = 0; i < N; i++)
if (a[i] == 0)
count++;

Таким образом, задача содержит 1 цикл for, мы проходим по нему, проверяем, является ли число нулем и увеличиваем счетчик. Анализируя этот код, видно, что i и count должны быть объявлены и приравнены к 0. Вот сравнение значений i и N, а вот добавление единицы [к значению i ] Вот сравнение a[i] c нулём, и этих сравнений N штук, N обращений к массиву. Увеличение счетчика является переменной. i увеличивается N раз, но счетчик может быть увеличен на любое число от 0 до N. Таким образом, частота этого события зависит от входных данных.

Может понадобиться модель для описания этой зависимости, или, может быть, в алгоритме найдутся другие, более затратные операции, и мы не будем беспокоиться об этой. Посмотрим на более сложную задачу.

int count = 0;
for (int i = 0; i < N; i++)
for (int j = i+1; j < N; j++)
if (a[i] + a[j] == 0)
count++;

Что с повторяемостью операций в этой программе, которая представляет задачу 2-SUM? Сколько пар целых чисел в сумме дают ноль? Потребуется проделать немного вычислений, чтобы обнаружить, что при увеличении i от 0 до n, а j от i+1 до n, число производимых сравнений или количество обращений к массиву равно двум, каждый раз, когда вычисляется ai или aj.

И этот оператор выполняется n-1 раз на первом проходе цикла, n-2 на втором, и так далее. Это сумма целых чисел от нуля до n-1, которая является дискретной суммой, равной половине n(n-1), так как мы вычисляем её дважды, то количество обращений к массиву равно n-1. Таким образом, мы можем продвигаться и получать эти действительные точные значения. Но уже это становится несколько утомительным занятием.

Обратимся к Тьюрингу, который, как и Бэббидж, знал, что необходима мера для количества работы, выполняемой процессом, он осознал, что нет необходимости проводить все расчеты. Полезно иметь грубую оценку. Таким образом, вы можете высчитывать повторяемость каждой операции, давать операциям веса и так далее. Возможно, стоит вычислять только самые затратные операции. Об этом Тьюринг говорил в 1947 году.

Сейчас мы делаем именно так: вместо того, чтобы рассчитывать все операции, мы определяем базовую операцию, которая является самой затратной, либо самой повторяемой, и по ней определяем время выполнения. Мы исходим из предположения, что время выполнения равно произведению этого значения на некоторую константу. Так, для данного случая мы выберем доступ к элементам массива. Это первое упрощение. А вторым упрощением будет то, что мы игнорируем члены низшего порядка в формулах.

Простой способ реализации называемый тильда-нотацией. Идея состоит в том, что при высоком значении N, значение n в кубе гораздо больше, чем само N. Разница настолько велика, что члены низкого порядка не влияют на результат. Получаем формулу: одна шестая от N в кубе, это хорошее приближение. Мы существенно упростили вычисления, отбросив члены низкого порядка. Свели всё к одной операции.



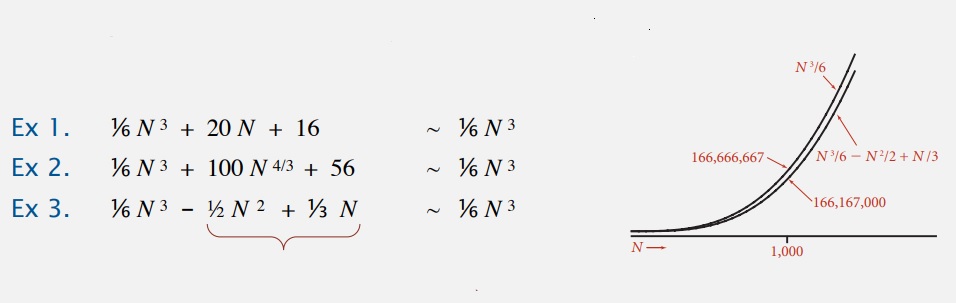
Вот техническое определение тильды: f(N)~g(N) значит, что предел f(N) к g(N) равен 1. Можете проверить, что условие соблюдается. Это сильно упрощает подсчет повторяемости. И если мы выбираем только одну операцию, то просто говорим о ~N квадрат, как в нахождении решения sum задачи. Это верно для большого значения N и не работает при малых значениях. Но это неважно, потому что нас интересует время выполнения при больших значениях N, а при малых значениях это время в любом случае невелико.

Используя модель затрат и приближение, можем сказать, что программа обращается к массиву ~N в квадрате раз, значит общее время выполнения равно ,по нашему предположению, N в квадрате, умноженное на константу. Хорошо, что насчет задачи 3-SUM?

int count = 0;
for (int i = 0; i < N; i++)
for (int j = i+1; j < N; j++)
if (a[i] + a[j] == 0)
count++;

Давайте решим реальную задачу. Теперь у нас тройной цикл, и значит нам надо решить более сложную комбинаторную задачу, но это не так уж сложно. Мы ищем несовпадающие способы выбора трех чисел из N, и это биномиальный коэффициент. Выполняя вычисления, вносим приближение и получаем 1/6 от N в кубе обращений к массиву для одного числа. В итоге получается N^3/3. Не вычисляем затраты на все операции — слишком много работы.



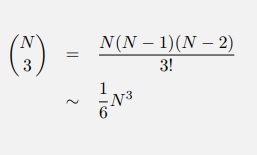
Мы выбрали наиболее затратную по времени операцию и упростили её в попытке получить модель для времени выполнения. В курсе мы не углубляемся в дискретную математику. Но есть некоторые базовые вещи, необходимые нам и легкие для понимания.

Очень часто нужно найти приближение дискретной суммы, как мы делали для суммы 1+2+...+N, или тройного цикла в задаче 3-SUM. Если вы владеете основами вычислений, то можете заменить сумму интервальным интегралом.



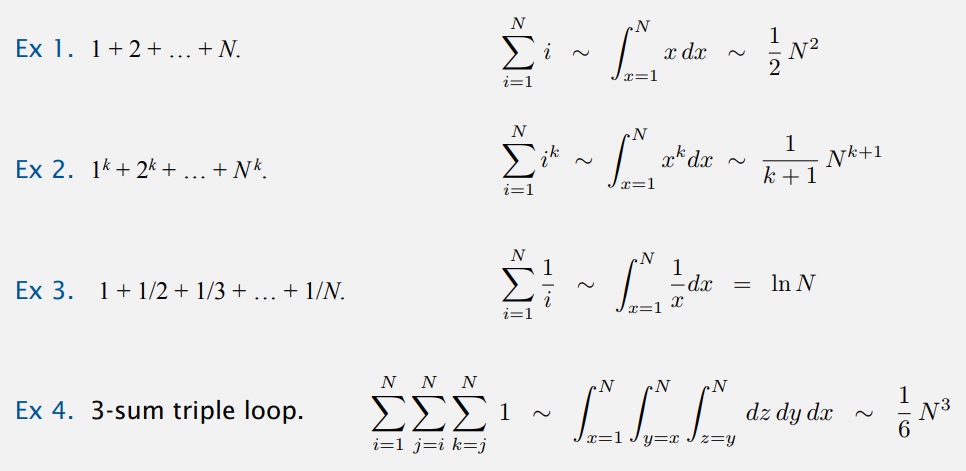
Этого обычно достаточно, или можно использовать формулу суммирования Эйлера-Маклорена для получения правильной аппроксимации. Размышляя таким образом, вы придете к тому, что сумма равна N^2/2. Или, что сумма единица плюс одна вторая, плюс одна треть и до единицы, деленной на N, которая преобразуется к интегралу в границах от единицы до N, от единицы деленной на x, равна натуральному логарифму от N.

Даже тройной цикл для 3-SUM, если есть опыт в интегралах, быстро сведется к N^3/6. Есть множество и других способов решения. Все мы рассматривать не будем. Но иногда будем на них ссылаться.

Кнут рассказал нам, что точные математические модели доступны. На практике, получаем сложные формулы. Иногда может потребоваться продвинутая математика, которой не владеют люди, впервые столкнувшиеся с алгоритмами. И в конце, аккуратные точные модели лучше оставить экспертам. В них слишком много деталей. С другой стороны, приближенные модели определенно полезны.
статьи IT, алгоритмы, теория программирования