Анализ алгоритмов: наблюдение

В первую очередь необходимо провести некоторые наблюдения о времени работы. Для анализа алгоритмов это легче, чем для многих научных дисциплин, как мы увидим. Для примера мы будем использовать задачу о сумме 3 чисел.

У этой задачи простая постановка. Если у вас есть N целых чисел, как много троек в сумме дают ноль? Для примера в файле 8ints.txt текст который содержит 8 целых чисел. Среди них есть три тройки в сумме дающие 0. 30 -40, 10. 30, -20, -10 и так далее. Наша цель написать программу, которая вычисляет это число для любого входного файла, любого набора N целых чисел.



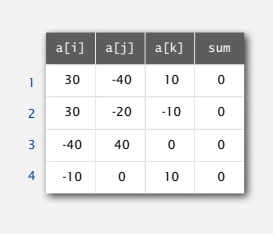
Это очень важные вычисления, которые глубоко связаны со многими задачами в вычислительной геометрии — разделом в компьютерных науках, который занимается алгоритмами и лежит в основе графики, фильмов и геометрических моделей любого рода. Т.е. это важная практическая задача. Но для нее просто написать код. Вы могли бы написать эту программу без больших усилий.

public class ThreeSum
{
 public static int count(int[] a)
 {
 int N = a.length;
 int count = 0;
 for (int i = 0; i < N; i++)
 for (int j = i+1; j < N; j++)
 for (int k = j+1; k < N; k++)
 if (a[i] + a[j] + a[k] == 0)
 count++;
 return count;
 }
 public static void main(String[] args)
 {
 int[] a = In.readInts(args[0]);
 StdOut.println(count(a));
 }
}

Это статический метод count, который принимает массив целых чисел. N — это целое число, длина массива. Мы начинаем с переменной count равной 0, и затем тройной цикл, который проверяет тройку i,j,k мы проходим i от 1 до n j от i+1 до n, и k от j+1 до n, так мы проверяем каждую тройку только раз. когда a[i]+a[j]+a[k] = 0, мы увеличиваем count на 1. И после этого тройного цикла count. И затем метод main, в этом простом классе просто читает все целые числа и выводит count.

Это грубый алгоритм для решения задачи суммы трех чисел. Сейчас нас интересует, как долго займет вычисление функции от n. Одни способ замерить время нашей программы это просто посмотреть на часы, если у вас есть секундомер, или часы в телефоне, или что-нибудь для измерения времени, можете использовать их если хотите.

В Java есть класс stopwatch, который вычисляет промежутки времени. Каждый раз когда вы запускаете программу, если она настроена на ввод разного размера, естественным будет просто запустить ее для больших задач. Для 8 целых эта программа занимает не много времени, для 1000 занимает пол секунды. Для 2000 занимает больше времени, 3.7 секунды. Запустим еще раз, все равно 3.7.

public static void main(String[] args)
{
 int[] a = In.readInts(args[0]);
 Stopwatch stopwatch = new Stopwatch();
 StdOut.println(ThreeSum.count(a));
 double time = stopwatch.elapsedTime();
}

Для 4000, мы каждый раз удваиваем размер входных данных, и это определённо занимает больше времени каждый раз. Есть программисты, которые тестируют время своих программ и могут достаточно просто и быстро оценить, когда они должны завершиться. Вместо того, чтобы каждый раз ждать, можно вычислить. Для 4000 выполнение занимает 30 секунд. Можно вычислить, сколько времени потребуется для 8000, сейчас покажу как.

Это эмпирический анализ, запущенный для разного входного размера и замеренного времени запуска.



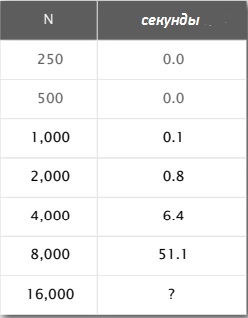
Если бы это была некоторая научная проблема, когда мы считаем что-то происходящее в окружающем мире — число муравьев в муравейнике то у нас было бы всего несколько точек данных, по которым мы бы пытались построить график. Получаем кривую подобную этой.



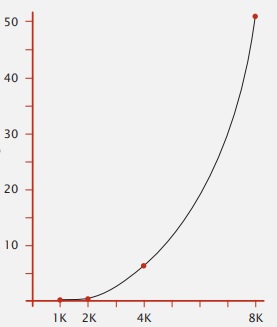
Много научных задач попадает под этот класс, и изображаются графиком. Очень часто получаем прямую линию. И наклон этой прямой, это ключ к тому, что происходит. В данном случае наклон прямой это 3.

Можно произвести регрессию и получить прямую через точки данных. И затем сделать расчеты чтобы показать что если вы получили прямую линию с наклоном B, то ваша функция пропорциональна aN^b. Это называется степенной зависимостью. И это верно для многих и многих научных задач включая большинство алгоритмов.

Немного математики. Прямая линия, т.к. мы делали график log-log по основанию 3, означает что lg(T(N)) = BlgN+C. И у нас есть наши эмпирические значения B и C и если затем возведем обе части этого уравнения в степень 2 и получим: T(N) = aN^b.



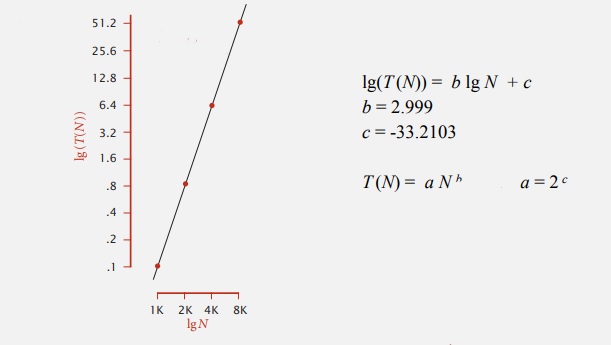
Т.е. прямо из наблюдений у нас есть неплохая модель времени работы нашей программы. Мы можем вывести и сделать расчёты, как мы и думали время работы примерно 10^-10N^3 секунд. Мы можем использовать эту гипотезу, чтобы сделать предсказание. Подставляем различные значения N. Для 16000 получается 400с.

Довольно много времени, но теперь мы можем пойти дальше и запустить этот эксперимент и удостовериться, что мы достаточно близко к этим 408 секундам. Можем сделать предсказание для 32000 или любого другого значения. Эта модель помогает делать предсказания без необходимости запускать эксперимент.

В большинстве компьютерных алгоритмов присутствует степенная зависимость, то есть зависимость от степени. Что мы можем сделать? Просто удвоить время размер водных данных каждый раз как делали, и взять отношение времени запуска для N и 2^N. И если вы сделаете это, то соотношение будет сходиться к константе. Действительно, log от отношения будет сходиться константе. Небольшими вычислениями можно это проверить.

Это очень простой способ проверить время работы. У нас есть быстрый способ оценить b, как оценить a? Мы можем запустить и решить это. Как только мы решили, что это экспонента трех, запустим это для больших N и получим достаточно точную модель, сравнимую с графиком. Это практически та же самая гипотеза и мы просто получаем результат запуская программу удваивая N каждый раз.

Много факторов влияют на время работы программы на компьютере, но ключевой эффект независим от того, что за компьютер используется. Это алгоритм и данные. Они определяют показатель степенной зависимости. И есть много системнозависимых эффектов. Что за оборудование вы используете. Быстрый ли у вас компьютер или медленный. Что за ПО. Что запущено на компьютере. Все эти факторы определяют константу a.

В настоящее время влияние оборудования и обеспечения сложно оценить точно. Но с другой стороны нам и не нужно ставить опыты над животными или лететь на другую планету, мы просто запускаем много экспериментов, чтобы разобраться с этими эффектами.
статьи IT, алгоритмы, теория программирования