Применение алгоритмов на примере перколяции

Мы рассмотрели эффективную реализацию алгоритма, которая может решить задачу объединения и поиска в предыдущей статье, а теперь поговорим о практическом применении. Есть огромное количество применений объединения и поиска. Мы говорили о динамическом соединении, но есть и много других примеров в вычислительных задачах.

Вот примерный список их:

• Перколяция.
• Игры (Go, Hex).
• Динамическое соединение.
• Наименьший общий предок.
• Эквивалентность конечных автоматов.
• Алгоритм Хошена-Копельмана в физике.
• Вывод полиморфного типа Хиндли-Милнера.
• Алгоритм минимального остовного дерева Краскала.
• Компиляция утверждений эквивалентности в Fortran.
• Морфологический атрибут открытия и закрытия.
• Функция bwlabel() (Matlab) для обработки изображений.

В самом низу одна важная задача — обработка изображений для понимания того, как помечать области изображения. В ней используется алгоритм минимального остовного дерева Крускала, это алгоритм обработки графов, который применяет объединение и поиск как подзадачу.

Есть алгоритмы в физике для понимания физических явлений, которые мы рассмотрим на примере. Поговорим о задаче перколяции. Это модель многих физических систем. Рассмотрим абстрактную модель и коротко обсудим, как это применяется в физических системах.

Итак рассмотрим сетку квадратов n x n, которые назовем участками. Будем говорить, что участок открыт — белый цвет на диаграмме — с вероятностью p или заблокирован — черный на диаграмме — с вероятность 1-p. Будем называть систему просачивающейся, если верх и низ соединены открытыми участками.



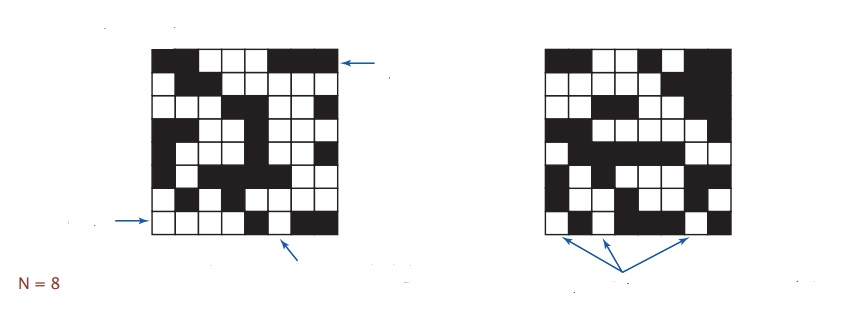
Так в системе слева, вы можете найти путь сверху вниз по белым квадратам, а система справа не просачивающаяся, нет пути сверху вниз по белым квадратам. Это модель для многих систем. Например в электронике. Можно представить, что открытые участки — проводники, а заблокированные изолированы. И тогда если есть проводимость сверху вниз, тогда устройство проводит электричество.

Или вы можете считать, что это вода, текущая сквозь поры некоторого вещества, где свободные участки просто пустые, а заблокированные участки заполнены материалом, и вода может или протечь сверху вниз, или нет. Или это может быть социальная сеть, где между людьми либо есть связь, либо нет, как и путь коммуникации от одной группы людей до другой через социальную сеть. Это всего лишь несколько примеров модели перколяции.

Мы поговорим о случайной модели, где участки свободны с заданной вероятностью. Вероятность, что участок свободен, низкая слева, и на этих двух примерах слева просачивания не будет. Недостаточно открытых участков для соединения верха и низа. Если вероятность высока, то будет много открытых участков, и будет просачивание. Будет много путей сверху вниз. Но посередине, где вероятность средняя, неизвестно будет ли просачиваться или нет.



Математический вопрос из этой модели такой: как мы узнаем будет ли перколяция? В этой задаче и многих подобных есть то, что называют фазой перехода. Ниже определенного значения перколяции не будет. А при превышении начнется просачивание. Порог между 2 состояниями очень резкий. При росте N существует некое значение вероятности, ниже которого почти наверняка просачивания не будет, а выше — точно будет. Задача найти значение.

Это пример математической модели с понятной задачей. Но это пороговое значение не найдено. Единственное решение — вычислительная модель для определения этой вероятности. Такая симуляция доступна благодаря алгоритму объединения и поиска.

Рассмотрим на примере, зачем нужны быстрые алгоритмы объединения и поиска. Проведем моделирование методом Монте-Карло. Мы задаем заблокированную сетку и случайно выбираем открытые участки. Каждый раз добавляя открытый участок, мы проверяем систему на предмет перколяции. Продолжаем до тех пор, пока не достигнем перколяции.

Процент отрытых участков будет оценкой порогового значения. Компьютер позволяет провести эксперимент более миллиона раз, если при этом мы сможем определять перколяцию. Моделирование методом Монте-Карло дает решение научной проблемы, которая не решена математически. Рассмотрим подробнее, как мы будем использовать модель динамической связности.

Мы создадим по объекту для каждого участка и пронумеруем их от нуля до N^2-1 Затем будем соединять, если они соединяются по открытым участкам. Модель перколяции слева соответствует модели справа, согласно тому как мы это делали. Можно сказать, что теперь нужно проверить, связан ли какой-либо участок снизу с каким либо участком сверху, используя для этого объединение-поиск.

Но это метод перебора с большими затратами по времени. Потому что ему потребуется N^2 операций поиска для проверки связности: для каждого участка сверху проверяется участок снизу. Слишком медленно. Вместо этого создадим по виртуальному участку сверху и снизу. И затем, если мы хотим узнать, просачивается система или нет, мы просто проверяем связан ли верхний виртуальный участок с нижним. Как мы моделируем открытие нового участка?

Для того, чтобы открыть участок мы соединяем его со всеми соседними открытыми участками. Несколько операций объединения, которые легко реализовать. Можем использовать тот же код, который разработали, чтобы решить задачу связности. Получаем результат, запуская моделирование достаточно много раз: порог перколяции примерно 0.592746. Используя алгоритм, получаем достаточно точный ответ.

Если используем медленный алгоритм объединения и поиска, то не сможем запустить его для очень больших задач и не получим точный ответ. Мы взяли важную задачу динамической связности и смоделировали её, чтобы понять, какого рода структуры данных и алгоритмы нам нужны для ее решения.

Мы рассмотрели несколько простых алгоритмов для решения задачи и быстро заметили, что они не походят для больших задач. И затем рассмотрели как их улучшить, чтобы получить эффективный алгоритм. Затем взялись за приложения, которые нельзя решить без эффективных алгоритмов. При работе над алгоритмами мы создаем математические модели, которые помогают понять свойства разрабатываемых алгоритмов. Мы тестируем модели в ходе экспериментов с целью улучшить алгоритмы, разработать лучшие алгоритмы и более специфические модели, пока не получим решение практических задач.