Теория игр: игроки

Продолжим с теорией игр: поговорим об определениях. Начнем с эгоистичных игроков и их взаимодействий. Давайте для начала поговорим о том, что мы подразумеваем под эгоистичными игроками. Мы не обязательно имеем в виду, что эти игроки враждебно настроены и не беспокоятся о том, что происходит с другими игроками. Мы имеем в виду, что эти игроки имеют мнения, предпочтения, и есть некоторое описание мира, каким может быть мир, и в различных описаниях игроки имеют различные предпочтения и различные полезности, как мы увидим.

Что мы подразумеваем под функцией полезности - это математическая мера, которая говорит нам, насколько игрока устраивает или не устраивает данная ситуация. Она описывает не только их отношение к различным событиям, так, например, завтра температура будет точно 25 градусов. Но на самом деле, это описывает предпочтения относительно распределения таких исходов. Поэтому она действительно отражает их отношение к неопределённости событий.

Так, например, если я скажу вам, что будет 25 градусов с вероятностью 0.7 и 24 градуса с вероятностью 0.3 у вас может сложиться мнение о том, насколько вам нравится это по сравнению с другими распределениями. И подход модели статистических решений, который лежит в основе современной теории игр, говорит, что вы будете пытаться действовать так, чтобы максимизировать вашу ожидаемую среднюю полезность. И поэтому это концепция, с которой мы должны освоиться.

И это неочевидно, что кто-то захочет использовать такой подход. Например, мы посмотрим на одномерный случай, когда все ваши предпочтения будут на одной шкале. Как мы увидим, эта шкала - это не то, что важно. В отличие от вероятности, полезности не должны лежать от нуля до единицы. Но они будут лежать в линейном измерении, и может быть, это неуместно. Например, у вас может быть некоторый уровень богатства и некоторая степень здоровья. И вы имеете на определенном уровне представление о благополучии, но корректно ли это сопоставлять их и иметь одну шкалу? Вы можете поставить это под вопрос.

Аналогично, зачем смотреть на ожидаемую величину, когда вы смотрите на неопределенность, почему посмотреть на ожидаемую величину - это уместный способ отразить ваше отношение? Итак, это не тривиальные утверждения, на самом деле, топологически они существенны, но есть очень долгая традиция, и возможно, самые известные ссылки на фон Неймана.

Теория фон Неймана Моргенштерна, которая является введением в современную теорию игр. В ней эти функции полезности выводятся из базовых предположений. Мы не будем углубляться, но мы просто хотим отметить эту проблему как нечто, что будет лежать в основе всего, что мы будем говорить о теории игр, и что действительно лежит в ее основе.

Очевидно, одно из самых явных базовых понятий теории игр - это игроки в игре. Кто принимает решения, это люди? Мы говорим о правительствах, ведущие переговоры о торговых соглашениях? Мы говорим о компаниях, выбирающих стратегии для разработки товаров? Хотим ли мы перейти к моделированию людей внутри фирмы, как противоположность компании в целом? Есть целый ряд вопросов о том, как мы собираемся выбирать игроков, но они будут основными фигурами в принятии решений в том, что мы собираемс делать. Далее мы должны решить, как мы будем моделировать действия.

Итак, что могут игроки, какие действия игроки могут предпринять? Когда мы говорим о ведении переговоров, можно решать, наносить ли удар. Когда мы думаем об инвестировании, может быть, что инвестор решает, сколько акций покупать или продавать, когда покупать или продавать их. Как они должны реагировать на других людей на рынке, как они должны принимать решения в зависимости от цен. Когда мы думаем об избирателях, как они голосуют.

Итак, есть целое множество действий, и мы будем аккуратно следить за тем, что мы моделируем необходимые действия. Наконец, платежи. Итак, что мотивирует игроков? Они беспокоятся просто о какой-то выгоде. Имеют ли для них значение другие игроки? Как они получают полезность как функцию от тех действий, которые привели к этому в контексте игры?

Существует 2 стандартных представления игры. Первый, известный как нормальная форма это очень простое и явное представление игры. Итак, она перечисляет, какие выгоды получают игроки как функцию от их действий. Обыкновенно считается, что игроки действуют одновременно, но стратегии, и мы будем говорить об этом более детально, могут заключать в себе много всего.

Альтернативное представление известно как экстенсивная форма, и она включает более явное регулирование времени в игре. То есть кто двигается в какой точке во времени. Это будет представлено часто как дерево. Так, например, в шахматах один игрок делает ход первым. Игрок с белыми фигурами обычно ходит первый, и игрок с черными может видеть ход первого игрока и ответить на него. И так далее.

Это лучше представить как дерево, а не в нормальной форме. Так лучше отследить, что игроки знают, когда делают ход. В покере кто-то делает ход первым. Он может сделать ставку, но другой игрок видит только ставку и не всегда карту, которую видит другой игрок. Итак, в некоторых случаях у нас будут последовательные игры, где игроки обладают различной информацией в различные моменты времени. Мы поговорим о явном моделировании.

Начнем с нормальной формы, и затем далее в курсе мы перейдем к экстенсивной форме и поговорим о связи между этими двумя формами игры более детально.

Итак, игры в нормальной форме. Каковы ключевые составляющие? Опять же, игроки. Мы будем говорить о конечном числе игроков. Так, от 1 до n, где n - это числи игроков. Обычно мы будем ставить индекс i, чтобы обозначить обобщенного игрока. Набор действий для игроков мы также будем записывать с i. Хорошо, мы представим таким образом действия игрока i, а затем поговорим о профилях действий, которые просто будут списком того, что каждый игрок делает. Например, они решают, кооперироваться или нет с другими игроками.

В дилемме заключенного, о которой мы будем говорить, функция полезности - это функция платежей, которая выглядит как функция от всех предпринятых в игре действий. Что такое платеж для различных игроков? Для каждого игрока i у нас есть функция, которая говорит нам, как они оценивают исходы игры. И опять же, как они оценивают их, это может заключать в себе многое. И это очень важно убедиться что у нас правильное представление о том, что на самом деле мотивирует людей. Хорошо.

Часто когда мы представляем игры в нормальной форме, очень простой способ это сделать - составить матрицу игры. Давайте посмотрим на самое стандартное представление очень простых игр. Запишем матрицу для игры с двумя игроками. У нас есть игрок 1, он будет ключевым игроком. Игрок 2 будет по столбцам. Они выбирают действия. Это будет представлено в колонке матрицы. И ячейки, внутри ячеек будут представлены платежи. Так, например, игра TCP Backoff, может быть записана как матрица следующим образом.

Игрок 1 может быть записан как C или D. Это выбор игрока 1, известного как игрок по строкам. Это игрок 2, по столбцам, и они представляют выбор, который они делают, и внутри ячеек - платежи различных игроков. Если игрок 1 кооперируется, и игрок 2 кооперируется, тогда эти платежи для двоих игроков. Первый платеж, игрока 1, второй платеж - игрока 2. Итак, это для игрока в столбцах, это - для игрока в строках. Ок? Тогда закончим, например, если игрок в строках выбирает D, а игрок в столбцах выбирает C, тогда мы получаем платеж 0 для игрока в строках и -4 для игрока в столбцах.



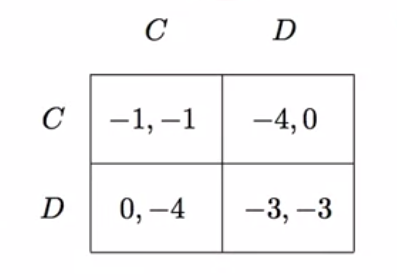
Матрица - это очень простой способ представления всех базовых элементов игры в нормальной форме наглядно, так что мы можем следить за стратегическим взаимодействием и за тем, что игроки делают как функция игры. Хорошо. Давайте поговорим о другой игре, которую мы не сможем записать в такой простой форме. Давайте подумаем о большом коллективном действии, игре.

Так, например, захочет ли население взбунтоваться против своего правительства. Здесь у нас намного больше игроков. Давайте представим, что у нас есть население из 10 миллионов игроков. Поэтому, очевидно, мы не собираемся записывать это как матрицу на нашем экране, поэтому мы будем подходить к этому более абстрактно. Но у нас будет 10 миллионов игроов, давайте сделаем всё очень просто. Здесь у них есть выбор: бунтовать или нет. Поэтому набор действий бинарный, два выбора.

Платежи - главное в этой игре. Что происходит? Предположим, чтобы бунт был успешным, нужно по крайней мере 2 миллиона человек участников. В этом конкретном стилизованном примере чем всё закончится? Мы можем представить успешный бунт, когда игрок выбирает путь 1, так что U_i профиля действий А равна 1. Если число людей здесь, число игроков j, таково, что они решили бунтовать, их число по крайней мере 2 миллиона. Итак, если мы имеем по крайней мере 2 миллиона бунтующих человек, тогда игрок i получает 1, и заметим здесь, что это верно, вне зависимости от того, являюсь ли я участником бунта, так что это игра, где нам важен конечный исход, а не получение полезности из участия.

Мы можем изменить это и сделать так, что люди буду получать удовольствие от участия или нести издержки. Хорошо, так что, что происходит, если ничего не получается. Здесь мы заканчиваем с менее чем 2000000 человек, тогда все зависит от того, участвовал ты в бунте или нет. Если вы, если игрок i был участником бунта, и он провалился, тогда он получает платеж -1. Так, может быть ситуация, где они будут наказаны правительством или они столкнуться с какими-то другими санкциями и они выберут путь 0, если окажутся неуспешными и они не участвовали, они не были среди бунтовавших людей.

Сейчас, очевидно, это очень стилизованно, но что это показывает, это то что игроки должны стратегически анализировать и предсказывать, что другие игроки собираются делать и их платежи зависят не только от того, что они делают, здесь именно была ситуация, где платеж i-го игрока зависел не только от того, участвовал ли он в бунте, но также от того, что делали другие игроки, и он может зависеть достаточно сложными путями от того, что делают все игроки в игре. Хорошо, подводя итог, в задании игр есть две разные формы: нормальная форма и экстенсивная.

В следующей статье мы начнем с ключевых моментов нормальной формы: игроков, действий и платежей. Позже, когда мы подойдем к экстенсивной форме, появится тайминг, информация и так далее. Это дополнительные вещи, которые нужны для более детального представления стратегического взаимодействия игроков.
статьи IT, теория игр, игры