Матрицы в математике

В математике матрица представляет собой прямоугольную таблицу чисел или, в более общем случае, таблицу, состоящую из абстрактных величин, которые можно добавлять и умножать. Матрицы используются для описания линейных уравнений, получения коэффициентов линейных преобразований и для записи данных, которые зависят от двух параметров. Матрицы могут быть добавлены, умножены и разложены различными способами, что делает их ключевым понятием в линейной алгебре и теории матриц.

В этой статье описаны матрицы реальных или комплексных чисел, если не указано иное.

Организация матрицы

Определения и обозначения

Горизонтальные линии в матрице называются строками, а вертикальные - столбцами. Матрица с m строками и n столбцами называется m-n матрицей (записывается m × n), а m и n называются ее измерениями. Размеры матрицы всегда задаются сначала количеством строк, а затем количеством столбцов.

Запись матрицы A, которая находится в i-й строке и в j-м столбце, называется i, j- ячейкой или ( i , j ) -й -й записью A. Это записывается как A i, j или A [ i, j ]. Сначала указывается строка, затем столбец.

Соглашение о том, что индексы i и j начинаются с 1, не является универсальным: некоторые языки программирования начинаются с нуля, и в этом случае мы имеем 0 ≤ i ≤ m - 1 и 0 ≤ j ≤ n - 1.

Матрица, в которой одно из измерений равно единице, часто называется вектором и интерпретируется как элемент реального координатного пространства. Матрица 1 × n (одна строка и n столбцов) называется вектор строки, и матрица m × 1 (один столбец и m строк) называется вектор столбца.

Пример


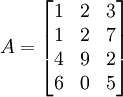
матрица 4 × 3 Элемент A [2,3] или 2,3 равен 7.

Добавление и умножение матриц

Сумма

Для заданных m-n матриц A и B их сумма A + B является матрицей m- n, вычисленной путем добавления соответствующих элементов (т. Е. ( A + B ) [ i, j ] = A [ i, j ] + B [ i, j ]). Например:



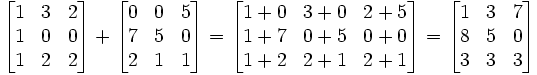
Еще одним, гораздо реже используемым понятием добавления матрицы является прямая сумма.

Скалярное умножение

Беря матрицу А и число с, скалярное умножение cA вычисляется умножением скаляр c по каждому элементу A (то есть ( cA ) [ i , j ] = cA [ i , j ]). Например:



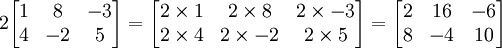
Матричное умножение

Умножение двух матриц корректно определено только в том случае, если количество столбцов левой матрицы совпадает с числом строк правой матрицы. Если A является матрицей m- by- n и B является матрицей n- by- p , то их матричное произведение AB является матрицей m- by- p ( m строк, p столбцов), определяемой как:

(AB) [i, j] = A [i, 1] B [1, j] + A [i, 2] B [2, j] + ... + A [i, n] B [n, j ] \! \ для каждой пары i и j .

Например:



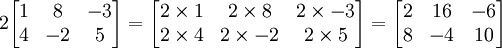
Эти две операции превращают множество M ( m , n , R ) всех m- byn матриц с действительными входами в вещественное векторное пространство размерности mn .

Умножение матриц имеет следующие свойства:

• ассоциативность
• правая дистрибутивность
• левая дистрибутивность

Важно отметить, что коммутативность обычно не имеет места; то есть, если заданы матрицы A и B и их произведение, то, как правило, AB ≠ BA .

Линейные преобразования, ранги и транспонирование

Матрицы могут удобно представлять линейные преобразования, потому что умножение матриц аккуратно соответствует составу карт, как будет описано далее. Это же свойство делает их мощными структурами данных в языках программирования высокого уровня.

Здесь и далее мы отождествляем R n с набором «столбцов» или n-y-1 матриц. Для каждого линейного отображения f : R n → R m существует единственная m- by- n матрица A такая, что f ( x ) = Ax для всех x в R n . Мы говорим, что матрица A «представляет» линейное отображение f . Теперь, если k- by- m матрица B представляет другое линейное отображение g : R m → R k , то линейное отображение g o f представляется BA. Это следует из вышеупомянутой ассоциативности умножения матриц.

В более общем смысле, линейное отображение из n- мерного векторного пространства в m- мерное векторное пространство представляется матрицей m- by- n при условии, что базы были выбраны для каждого.

Ранг матрицы А является размерностью изображения линейной карты, представленной буквой A; это то же самое, что и размер пространства, генерируемого строками A, а также то же, что и размер пространства, генерируемого столбцами A.

Транспонировать m- by- n- матрицу A - это n- by- m- матрица A tr (также иногда записываемая как A T или t A ), образованная путем преобразования строк в столбцы и столбцов в строки, то есть A tr [ i , j ] = A [ j , i ] для всех индексов i и j . Если A описывает линейное отображение относительно двух базисов, то матрица A tr описывает транспонирование линейного отображения относительно дуальных базисов.

Мы имеем ( A + B ) tr = A tr + B tr и ( AB ) tr = B tr A tr.

Специальные типы матриц

Во многих областях математики возникают матрицы с определенной структурой. Несколько важных примеров

• Симметричные матрицы таковы, что элементы, симметричные относительно главной диагонали (от левого верхнего до нижнего правого), равны, то есть a i, j = a j, i.
• Кососимметричные матрицы таковы, что симметричные относительно главной диагонали элементы являются отрицательными друг от друга, то есть a i, j = - a j, i. В кососимметричной матрице все диагональные элементы равны нулю, то есть a i, i = 0.
• Эрмитовы (или самосопряженные) матрицы таковы, что симметричные относительно диагонали элементы являются друг другом комплексные конъюгаты, то есть a i, j = a * j, i, где верхний индекс '*' означает комплексное сопряжение.
• Матрицы Теплица имеют общие элементы на диагоналях, то есть a i, j = a i + 1, j + 1.
• Стохастические матрицы - это квадратные матрицы, столбцы которых векторы вероятности; они используются для определения цепей Маркова.

История

Изучение матриц имеет долгую историю. Латинские квадраты и магические квадраты изучались с доисторических времен.

Матрицы имеют долгую историю применения в решении линейные уравнения. Лейбниц, один из двух основателей исчисления, разработал теорию детерминанта в 1693. Крамер развил теорию дальше, представляя Правило Крамера в 1750. Карл Фридрих Гаусс и Вильгельм Джордан разработали МетодГаусса-Иордана в 1800-х гг.

Термин «матрица» был впервые введен в 1848 Джей Джей Сильвестром. Кейли, Гамильтон, Грассман, Фробениус и фон Нейман являются одними из известных математиков, которые работали над теорией матриц.

Применение

Транспорт

Если вам дается список городов (или пунктов назначения, узлов и т. д.) и есть рейсы (или дороги, соединения и т. д.) Из города a в город b , то можно построить квадратную матрицу с городами индексированно каждой стороне матрицы. Каждая запись M a , b устанавливается в 1, если есть соединение от a до b ; это 0 в противном случае. Если существует обратное соединение, идущее от b к a , то также M b , a = 1. Во многих случаях соединение a к b может не быть двунаправленным, то есть M a , b = 1 не обязательно означает, что M b , а = 1.

Умножая матрицу M на себя, получаем M 2 . Матрица M 2 покажет, можно ли перейти от а к б через третий город. Если ( M 2 ) a , b = 1, то существует один третий город c, который действует как переход, то есть вы можете перейти от a к c и затем из c в b . Если ( M 2 ) a , b = n , то таких переходов n .

Шифрование

Матрицы могут быть использованы для шифрования числовых данных. Шифрование выполняется путем умножения матрицы данных на ключевую матрицу. Расшифровка выполняется простым умножением зашифрованной матрицы на обратный ключ.

Компьютерная графика

Матрицы преобразования 4х4 обычно используются в компьютерной графике. Верхняя левая часть матрицы преобразования 3x3 состоит из новых осей X, Y и Z координатного пространства после преобразования.