|
|
Определитель (детерминант) матрицы 2 на 2
Давайте разберемся, как использовать матрицу для решения системы одновременных уравнений. Определитель - это квадратная таблица из чисел (внутри пары вертикальных линий), которую можно привести к определенному числу. Ниже приведен пример определителя 3 × 3 (он имеет 3 строки и 3 столбца).
11 0 8
Результатом умножения, а затем упрощения элементов является одно число (скалярная величина).
−4 5 -3 0 2 3 Вычисление определителя 2 × 2 В общем случае мы находим значение определителя 2 × 2 с элементами a, b, c, d следующим образом:
a b = ad - cb
c d Мы перемножаем диагонали, потом вычитаем. Пример 1
4 2
= 4*8 - 2*3 = 32 - 6 = 26
3 8 Конечным результатом является одно число. Мы увидим, как развернуть 3 на 3 определитель ниже. Использование определителей для решения систем уравнений Мы можем решить систему уравнений при помощи определителей, но это будет очень утомительно для больших систем. Мы будем делать только 2 2 и 3 3 системы при помощи определителей. Правило Крамера Решение (x, y) системы a1x + b1y = c1 a2x + b3y = c2 может быть найдено с помощью определителей: 
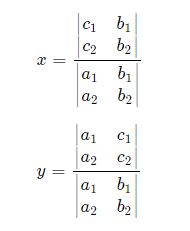
Пример 2 Решите систему уравнений с помощью метода Крамера x − 3y = 6 2x + 3y = 3 Сначала мы расставляем коэффициенты, а потом применяем правило Крамера: 
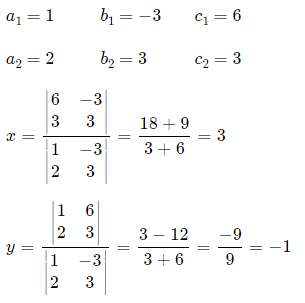
Поэтому решение будет (3,-1).  Автор этого материала - я - Пахолков Юрий. Я оказываю услуги по написанию программ на языках Java, C++, C# (а также консультирую по ним) и созданию сайтов. Работаю с сайтами на CMS OpenCart, WordPress, ModX и самописными. Кроме этого, работаю напрямую с JavaScript, PHP, CSS, HTML - то есть могу доработать ваш сайт или помочь с веб-программированием. Пишите сюда.  заметки, математика, матрица, определитель, решение задач |
|
Программы на заказ
Отзывы
Контакты| © upread.ru 2013-2021 При перепечатке активная ссылка на сайт обязательна. |
