Аналитическая геометрия

Аналитическая геометрия - это раздел алгебры, великое изобретение Декарта и Ферма, которое занимается моделированием некоторых геометрических объектов, таких как линии, точки, кривые и так далее. Это математический предмет, который использует алгебраическую символику и методы для решения задач. Он устанавливает соответствие между алгебраическими уравнениями и геометрическими кривыми. Альтернативным термином, который используется для представления аналитической геометрии, является “координатная геометрия”.

В нем рассматриваются некоторые важные темы, такие как средние точки и расстояние, параллельные и перпендикулярные линии на координатной плоскости, сегменты разделительной линии, расстояние между линией и точкой и так далее. Изучение аналитической геометрии важно, так как оно дает знания для следующего уровня математики. Это традиционный способ обучения логическому мышлению и навыкам решения проблем. В этой статье давайте обсудим термины, используемые в аналитической геометрии, формулы, декартову плоскость, аналитическую геометрию в трех измерениях, ее приложения и некоторые решаемые задачи. Для программиста довольно важно знать хотя бы основы этого предмета.

Содержание:

• Определение
• Плоскости
• Координаты
• Декартова плоскость
• Формулы
• Аналитическая геометрия в 3D
• Приложения
• Примеры задач

Что такое аналитическая геометрия?

Аналитическая геометрия - это та ветвь алгебры, в которой положение точки на плоскости может быть определено с помощью упорядоченной пары чисел, называемых координатами. Это также называется координатной геометрией или декартовой геометрией. Аналитическая геометрия противоречит синтетической геометрии, где не используются координаты или формулы. Это считается аксиомой или допущением, позволяющим решать проблемы. Но в аналитической геометрии он определяет геометрические объекты, используя локальные координаты. Он также использует алгебру для определения этой геометрии.

Координатная геометрия используется как в двумерной, так и в трехмерной геометрии. Он используется для представления геометрических фигур. Давайте изучим терминологию, используемую в аналитической геометрии, такую как;

• Плоскость
• Координаты

Плоскости

Чтобы понять, насколько важна и полезна аналитическая геометрия, сначала нам нужно узнать, что такое плоскость? Если плоская поверхность продолжается бесконечно в обоих направлениях, она называется плоскостью. Итак, если вы найдете какую-либо точку на этой плоскости, ее легко найти с помощью аналитической геометрии. Вам просто нужно знать координаты точки в плоскости X и Y.

Координаты

Координаты - это две упорядоченные пары, которые определяют местоположение любой заданной точки на плоскости. Давайте разберемся в этом с помощью приведенной ниже таблицы.



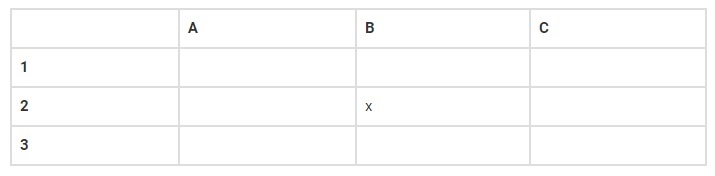
В приведенной выше сетке столбцы помечены как A, B, C, а строки - как 1, 2, 3. Расположение буквы x равно B2, т. е. Столбец B и строка 2. Итак, B и 2-координаты этого поля, x.

Поскольку в каждом столбце и строках есть несколько полей, но только в одном поле есть точка x, и мы можем найти ее местоположение, определив пересечение строки и столбца этого поля. В аналитической геометрии существуют различные типы координат. Некоторые из них заключаются в следующем:

• Декартовы координаты
• Полярные координаты
• Цилиндрические координаты
• Сферические координаты

Давайте вкратце обсудим все эти типы координат здесь.

Декартовы координаты

Наиболее известной системой координат является используемая декартова система координат, где каждая точка имеет координаты x и y, выражающие ее горизонтальное положение и вертикальное положение соответственно. Они обычно рассматриваются как упорядоченная пара и обозначаются как (x, y). Мы также можем использовать эту систему для трехмерной геометрии, где каждая точка представлена упорядоченной тройкой координат (x, y, z) в евклидовом пространстве.

Полярные координаты

В случае полярных координат каждая точка на плоскости обозначается расстоянием " r " от начала координат и углом θ от полярной оси.

Цилиндрические координаты

В случае цилиндрических координат все точки представлены их высотой, радиусом от оси z и углом, проецируемым на плоскость xy относительно горизонтальной оси. Высота, радиус и угол обозначаются h, r и θ соответственно.

Сферические координаты

В сферических координатах точка в пространстве обозначается ее расстоянием от начала координат ρ, углом, проецируемым на плоскость xy относительно горизонтальной оси θ, и другим углом относительно оси z φ.

Декартова плоскость

В координатной геометрии каждая точка, как говорят, расположена только на координатной плоскости или декартовой плоскости.

Посмотрите на рисунок ниже.


Координатная плоскость в аналитической геометрии

Приведенный выше график имеет оси x и y в качестве масштаба. Ось x проходит поперек плоскости, а ось Y проходит под прямым углом к оси x. Это похоже на коробку, описанную выше.

Давайте узнаем больше о координатах:

Начало координат: Это точка пересечения оси x и оси y. И ось x, и ось y в этой точке равны нулю.

Значения различных сторон оси:

ось x – Значения с правой стороны этой оси являются положительными, а значения с левой стороны - отрицательными.

ось y – Значения выше начала координат положительные, а ниже начала координат отрицательные.

Чтобы найти точку: нам нужны два числа, чтобы найти плоскость в порядке записи сначала местоположения оси X, а затем оси Y. И то, и другое укажет единственное и уникальное положение на плоскости. Вам нужно обязательно следовать порядку точек на плоскости, т. е. координата x всегда является первой из пары. x,y.

Если вы посмотрите на рисунок выше, точка А имеет значение 3 по оси x и значение 2 по оси Y. Это прямоугольные координаты точки А, представленные в виде 3,2.

Используя декартовы координаты, мы можем определить уравнение прямых, уравнение плоскостей, квадратов и чаще всего в трехмерной геометрии. Основная функция аналитической геометрии заключается в том, что она определяет и представляет различные геометрические фигуры численным способом. Он также извлекает числовую информацию из фигур.

Формулы аналитической геометрии

Графики и координаты используются для поиска измерений геометрических фигур. В аналитической геометрии существует много важных формул. Поскольку наука и техника включают в себя изучение скорости изменения различных величин, это помогает показать взаимосвязь между задействованными величинами. Раздел математики, называемый “вычисления”, требует четкого понимания аналитической геометрии. Здесь некоторые из важных из них используются для определения расстояния, наклона или для нахождения уравнения прямой.

Формула расстояния

Пусть двумя точками являются A и B, координаты которых должны быть (x1,y1) и (x2,y2) соответственно.

Таким образом, расстояние между двумя точками выглядит как

d = √[(x2-x1)2+(y2-y1)2]

Формула теоремы о средней точке

Пусть A и B - некоторые точки на плоскости, которые соединяются в линию, имеющую координаты (x1,y1) и (x2,y2) соответственно. Предположим, что M(x,y) - середина прямой, соединяющей точки A и B, тогда ее формула:

Mx,y = [(x1+x2/2),(y1+y2/2)]

Формула угла

Пусть две линии имеют наклон m1 и m2, а θ-угол, образованный между двумя линиями A и B, который представлен в виде;

tan θ = m1-m2/1+m1m2

Аналитическая геометрия в трех измерениях

В этом мы рассматриваем тройки (a, b,c), которые являются действительными числами, и называем это множество трехмерным числовым пространством и обозначаем его через R’. Все элементы в тройке называются координатами.

Давайте посмотрим, как трехмерное числовое пространство представлено на геометрическом пространстве.

В трехмерном пространстве мы рассматриваем три взаимно перпендикулярные линии, пересекающиеся в точке O. Эти линии обозначены координатными осями, начиная с 0, и на каждой из них установлены одинаковые числовые шкалы.

Приложения аналитической геометрии

Аналитическая геометрия широко используется в таких областях, как инженерия и физика. Кроме того, он широко используется в таких областях, как космическая наука, ракетостроение, авиация, космические полеты и так далее. Аналитическая геометрия сделала возможным многое, например, следующее:

• Мы можем определить, являются ли данные линии перпендикулярными или параллельными.
• Мы можем определить среднюю точку, уравнение и наклон отрезка прямой.
• Мы можем найти расстояние между точками.
• Мы также можем определить периметр области многоугольника, образованного точками на плоскости.

Задачи аналитической геометрии

Пример 1:

Как называется точка пересечения осей X и Y?

Решение:

Точка пересечения оси X и оси Y, называемая началом координат, и X и ось Y в этой точке равны 0.

Пример 2:

Найдите расстояние между двумя точками A и B таким образом, чтобы координаты A и B равнялись 5, -3 и 2, 1.

Решение:

Учитывая это, координаты являются:

A = 5, -3 = (x1, y1)

B = 2, 1 = (x2,y2)

Формула для нахождения расстояния между двумя точками приводится в виде:

Расстояние,d = √[(x2-x1)2+(y2-y1)2]

d = √[(2-5)2+1- (-3)2]

d =√[(-3)2+42]

d =√9+16

d =√25
d = 5

Таким образом, расстояние между двумя точками A и B равно 5.