Биномиальное распределение с примерами

Биномиальное распределение - это распределение вероятностей, применимое к биномиальным экспериментам. Это количество успехов в определенном количестве попыток. Биномиальное распределение можно представить как распределение вероятностей числа угадываний при подбрасывании монеты в конкретном эксперименте, состоящем из фиксированного числа подбрасываний. В материале мы изучим биномиальное распределение с помощью примеров. Если вы начинающий специалист по обработке данных, с нетерпением ожидающий лучшего изучения/понимания биномиального распределения, этот пост может быть очень полезен. Да и для программистов освежить знания по математике, статистике и теории вероятностей тоже полезно.



Содержание

• Введение
• Что такое случайная величина?
• Что такое биномиальная случайная величина?
• Что такое биномиальный эксперимент?
• Что такое биномиальное распределение?
• Реальные примеры биномиального распределения
• Выводы

Введение

Биномиальное распределение - это дискретное распределение вероятностей, которое представляет вероятности биномиальных случайных величин в биномиальном эксперименте. Биномиальное распределение определяется как распределение вероятностей, связанное с лпределенным экспериментом, где случайная величина определяет, сколько успехов или неудач произошло в этом пространстве выборки. Для специалистов по обработке данных и специалистов в других областях важно понимать эту концепцию, поскольку биномы часто используются в бизнес-приложениях.

Что такое случайная величина?

Случайная переменная представляет собой переменную, которая может принимать случайные значения в эксперименте. Допустим, случайная величина, представляющая количество дефектных предметов, найденных в 100 предметах, выбранных случайным образом. Здесь 100 предметов представляют собой 100 испытаний. Может быть проведено несколько экспериментов, включающих случайную выборку 100 предметов и подсчет количества дефектных предметов.

• В 1-м эксперименте 5 предметов были признаны дефектными.
• Во 2-м эксперименте 9 предметов были признаны дефектными.

В приведенном выше эксперименте количество предметов, признанных дефектными, можно назвать СЛУЧАЙНОЙ величиной. Случайная величина также представлена буквой X. В вышеупомянутых экспериментах X принимает значения 5 и 9.

Когда значение случайной величины может принимать только конечные значения, случайную величину также можно назвать случайной дискретной переменной. Когда значение случайной величины может принимать бесконечные значения, случайную величину также можно назвать случайной непрерывной переменной.

Все возможные значения (или результаты), которые может принимать случайная величина, также называются пространством выборки.

Что такое биномиальная случайная величина?

В биномиальном эксперименте результат каждого испытания в эксперименте может принимать одно из двух значений, которые являются либо успехом, либо неудачей. Каждое испытание в биномиальном эксперименте также можно назвать испытанием Бернулли. Для одного испытания биномиальное распределение также можно назвать распределением Бернулли.

Другими словами, результат каждого испытания классифицируется в соответствии с двумя уровнями категориальной переменной. Вот несколько примеров испытаний Бернулли:

• При подбрасывании монеты результатом может быть либо успех (ОРЕЛ), либо неудача (РЕШКА).
• При поиске дефектных товаров результатом может быть либо успех (товар неисправен), либо неудача (товар не неисправен).
• При броске кубика результатом может быть либо успех (одно из чисел из 1-6 (скажем, шесть-6)), либо неудача (любое из чисел, кроме) в противном случае.

Результат интереса к испытанию эксперимента часто называют успехом.

Биномиальной случайной величиной может быть число успехов в эксперименте, состоящем из N испытаний. Таким образом, ниже приведены некоторые примеры биномиальной случайной величины:

• Количество успехов (голов) в эксперименте из 10 попыток подбрасывания монеты; Здесь пространство выборки равно {0, 1, 2, ...10}
• Количество успехов (шесть) в эксперименте из 10 попыток прокатки штампа; Здесь пространство для выборки равно {0, 1, 2, ...10}
• Количество успехов (дефектных предметов) в эксперименте из 10 попыток изучения 10 предметов; Здесь пространство выборки равно {0, 1, 2, ...10}

Что такое биномиальный эксперимент?

Биномиальный эксперимент представляет собой биномиальную случайную величину X, которая подсчитывает число "n" успехов в N испытаниях, когда каждое испытание имеет только два результата, успех и неудачу. Таким образом, эксперимент может состоять из 1 испытания, 5 испытаний, 10 испытаний, 20 испытаний и т.д. Наблюдая за примерами из реального мира, эксперимент может заключаться в подбрасывании монеты 10 раз (10 испытаний), взятии 10 предметов для проверки, являются ли они дефектными, и т. д. Если эксперимент состоит только из одного испытания, которое имеет только два результата, таких как успех или неудача, испытание называется испытанием Бернулли.

Требования к тому, чтобы случайный эксперимент был биномиальным экспериментом, следующие:

• Фиксированное число (n) испытаний
• Каждое испытание должно быть независимым от других
• Каждое испытание должно привести к одному из двух возможных результатов, называемых "успехом" (результат интереса) или "неудачей".
• Существует постоянная вероятность (p) успеха для каждого испытания, дополнением к которой является вероятность (1 – p) неудачи, иногда обозначаемая как q = (1 – p)

Что такое биномиальное распределение?

Биномиальное распределение - это тип дискретного распределения вероятностей, представляющий вероятности различных значений биномиальной случайной величины (X) в повторных независимых N испытаниях в эксперименте. Таким образом, в эксперименте, включающем бросание монеты 10 раз (N), биномиальная случайная величина (количество голов, представленных как успехи) может принимать значение 0-10, а биномиальное распределение вероятностей - это распределение вероятностей, представляющее вероятности случайной величины, принимающей значение 0-10.

Вероятность того, что случайная величина X с биномиальным распределением B(n,p) равна значению k, где k = 0, 1,...., n, задается следующей формулой:



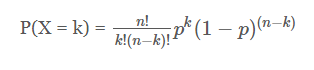
Среднее значение и дисперсия биномиального распределения эксперимента с n количеством испытаний и вероятностью успеха в каждом испытании p следующие:

Среднее значение = np
Дисперсия = np(1-p)


В биномиальном эксперименте, состоящем из N испытаний, все испытания являются независимыми, и образец рисуется с заменой. Если выборка нарисована без замены, это называется гипергеометрическим распределением.

Реальные примеры биномиального распределения

Вот несколько реальных примеров биномиального распределения:

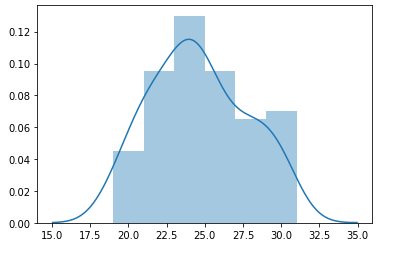
• Бросание кубика: Вероятность получения числа шесть (6) (0, 1, 2, 3...50) при броске кубика 50 раз; Здесь случайная величина X - это количество "успехов", то есть количество раз, когда происходит шесть. Вероятность получить шестерку равна 1/6. Биномиальное распределение может быть представлено в виде B(50,1/6). На приведенной ниже диаграмме представлено биномиальное распределение для 100 экспериментов.
  
• Бросание монеты: Вероятность получения количества голов (0, 1, 2, 3...50) при подбрасывании монеты 50 раз; Здесь случайная величина X - это количество "успехов", то есть количество выпадений орла. Вероятность получить орел равна 1/2. Биномиальное распределение можно представить в виде B(50,0,5). На приведенной ниже диаграмме представлено биномиальное распределение для 100 экспериментов.
  
• Дефектные изделия: Вероятность обнаружения количества дефектных изделий (0, 1, 2, 3...30) при проверке 30 раз; Здесь случайная величина X - это количество "успехов", то есть количество раз, когда обнаруживается дефектный товар. Вероятность обнаружения дефектного элемента равна p. Биномиальное распределение может быть представлено в виде B(30, p)
• Человек, страдающий какой-либо болезнью: Вероятность обнаружения 0 или более человек, страдающих определенной болезнью, при обследовании 100 человек; Здесь случайная величина X - это число "успехов", то есть число людей, страдающих какой-либо болезнью. Вероятность нахождения человека, страдающего какой-либо болезнью, говорит, п. Биномиальное распределение может быть представлено в виде B(100,p)
• Пример употребления алкоголя с высоким риском: Вероятность обнаружения пьющих с высоким риском при обследовании 1000 человек. Здесь случайная величина X - это количество "успехов", то есть количество студентов, которые являются пьющими с высоким риском. Мы можем использовать биномиальное распределение вероятностей (т. Е. биномиальную модель) для описания этой конкретной переменной. Допустим, вероятность/доля пьющих с высоким риском составляет 0,35 или 35 %. Биномиальное распределение может быть представлено в виде B(1000,0.35)
• Число избирателей-женщин: Вероятность нахождения избирателей-женщин при опросе 100 избирателей. Здесь случайная величина X - это число "успехов", то есть число избирателей женского пола. Мы можем использовать биномиальное распределение вероятностей (т. Е. биномиальную модель) для описания этой конкретной переменной. Допустим, вероятность/доля избирателей женского пола составляет 0,45 или 45 %. Биномиальное распределение может быть представлено в виде B(100,0.45)
• Студенты, сдающие экзамены: Вероятность нахождения студентов, сдавших экзамены, при обследовании 50 студентов. Здесь случайная величина X - это количество "успехов", то есть количество студентов, сдавших экзамены. Допустим, вероятность/доля студентов, сдающих экзамены, составляет 0,78 или 78 %. Биномиальное распределение может быть представлено в виде B(50,0.78)
• Водители, не имеющие страховки на автомобиль: Вероятность найти водителей, у которых нет страховки на автомобиль, при обследовании 100 водителей. Здесь случайная величина X - это количество "успехов", то есть количество водителей, у которых нет страховки на автомобиль. Допустим, вероятность/доля водителей, не имеющих автострахования, составляет 0,2 или 20%. Биномиальное распределение может быть представлено в виде B(100,0.20)
• Количество правильных ответов на вопросы с множественным выбором: Вероятность получения правильных ответов из 20 вопросов с множественным выбором, когда один из 4 вариантов был выбран произвольно. Здесь случайная величина X - это количество "успехов", то есть количество правильных ответов. Допустим, вероятность/доля правильного ответа составляет 1/4, 0,25 или 25 %. Биномиальное распределение может быть представлено в виде B(20,0.25)

Выводы

Вот краткое изложение того, что вы узнали в этом посте в отношении биномиального распределения:

• Биномиальное распределение - это дискретное распределение вероятностей, представляющее вероятности биномиальной случайной величины
• Биномиальная случайная величина представляет собой количество успехов в эксперименте, состоящем из фиксированного числа независимых испытаний, выполняемых в определенной последовательности.
• Эксперимент по биномиальному распределению будет состоять из фиксированного числа независимых испытаний, обозначаемых буквой N.
• Одно испытание в биномиальном эксперименте также называется испытанием Бернулли.
• Биномиальное распределение вероятностей измеряет вероятность количества успехов, которые могут произойти в нескольких экспериментах из N испытаний.