Двоичные числа и двоичная математика

Двоичная система счисления является альтернативой десятичной (на базе числа 10) системе счисления, которую мы используем каждый день. Двоичные числа важны, потому что их использование вместо десятичной системы упрощает проектирование компьютеров и связанных с ними технологий. Самым простым определением двоичной системы счисления является система нумерации, которая использует только две цифры: 0 и 1 — для представления чисел, вместо того, чтобы использовать цифры от 1 до 9 плюс 0.

Как пример перевода между десятичными и двоичными числами, вы можете использовать таблицу ниже:



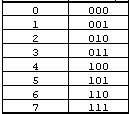
Обратите внимание, что 0 и 1 одинаковы в любой системе, но начиная с 2, все меняется. Например, десятичная 2 выглядит как 10 в двоичной системе. 0 равно нулю, как вы ожидали.

Вот как перевести между двоичным и десятичным. В каждом двоичном числе первая цифра, начинающаяся с правой стороны, может быть равна 0 или 1. Но если вторая цифра равна 1, то она представляет число 2. Если это 0, то это просто 0. Третья цифра может быть равна 4 или 0. Четвертая цифра может равняться 8 или 0. И так далее. Если вы запишите десятичные значения каждой из цифр, а затем сложите их, у вас будет десятичное значение двоичного числа. В случае двоичного 11 в первой позиции есть 1, что равно 1, а затем еще 1 во второй позиции, то есть 2. Добавьте 2 + 1 вместе, и вы получите 3.

По мере того как числа становятся больше, новые цифры добавляются слева. Чтобы определить значение цифры, подсчитайте количество цифр слева от нее и умножьте это число на 2. Например, для цифрового числа 100, чтобы определить значение 1, подсчитайте количество цифр до слева от 1 и умножьте это число на 2. Число равно 2 × 2, что равно 4. Общее значение двоичного числа 100 равно 4, поскольку числа слева от 1 равны 0. Теперь вы знаете, как считать цифровые числа, но как их сложить и вычесть? Двоичная математика похожа на десятичную математику. Добавление двоичных чисел выглядит так, как показано в поле справа вверху.

Чтобы сложить двоичные числа, сделайте следующее: начните с правой стороны, как и в обычной математике. В колонке чисел с правой стороны добавьте 0 + 1, Как обычно, чтобы получить 1. Запишите 1 в область решения. Но во втором столбце 1 + 1 не равен 2, он равен двоичному 2, который записан 10. Каждый раз, когда вы добавляете 1 + 1 в двоичной математике, записывайте 0 и переносите 1 в следующий столбец. В третьем столбце теперь у вас есть 0 + 1 плюс 1, которую вы перенесли. Согласно нашему правилу, это равно 0, поэтому напишите 0 и перенесите 1 в следующий столбец. Теперь в четвертом столбце у вас есть 1 + 1, + 1, который вы перенесли. Каждый раз, когда у вас есть столбец, который складывается до десятичного числа 3, вы записываете 1 в области решения и переносите 1. В пятом столбце у вас есть только 1, который вы перенесли, поэтому вы записываете 1 в пятом столбце. решения. Та же самая проблема в десятичной математике - 10 + 15 = 25.

Компьютеры полагаются на двоичные числа и двоичную математику, потому что это значительно упрощает их задачи. Поскольку существует только две возможности (0 и 1) для каждой цифры, а не 10, легче хранить или манипулировать числами. Простое устройство, такое как переключатель или транзистор, который имеет два различных состояния, таких как “on” и “off”, может стать блоком памяти или частью калькулятора. Компьютеры нуждаются в большом количестве транзисторов, чтобы выполнить все это, но все же легче и дешевле делать вещи с двоичными числами, а не с десятичными числами.

Первоначально компьютеры использовались в основном в качестве калькуляторов, но позже они стали применяться для манипулирования другими формами информации, такими как слова и картинки. В каждом случае инженеры и программисты садились и решали, как они будут представлять новый тип информации в двоичной форме. Наиболее популярный способ перевода алфавита в двоичные числа - американский стандартный код для обмена информацией или ASCII.

Хотя это довольно сложно сделать, звуки и изображения также могут быть преобразованы в двоичные числа. Они должны быть разделены на небольшие элементы ("сэмплы" в аудио или "пиксели" для изображений), а затем каждому элементу должен быть присвоен номер. Результатом является огромный массив двоичных чисел, и объем всех этих данных является одной из причин, почему файлы изображений на компьютере так велики, и почему он относительно медленно просматривать видео или загружать аудио через подключение к интернету.

Двоичные и десятичные в программировании

Одна из самых популярных задач программирования - это перевод между различными системами счисления. Вот, например, как с на Java реализуется алгоритм перевода, который мы расписали выше:

public static void convertBinary(int num){
     int binary[] = new int[30];
     int index = 0;
     while(num > 0){
       binary[index++] = num%2;
       num = num/2;
     }
     for(int i = index-1;i >= 0;i--){
       System.out.print(binary[i]);
     }
  }

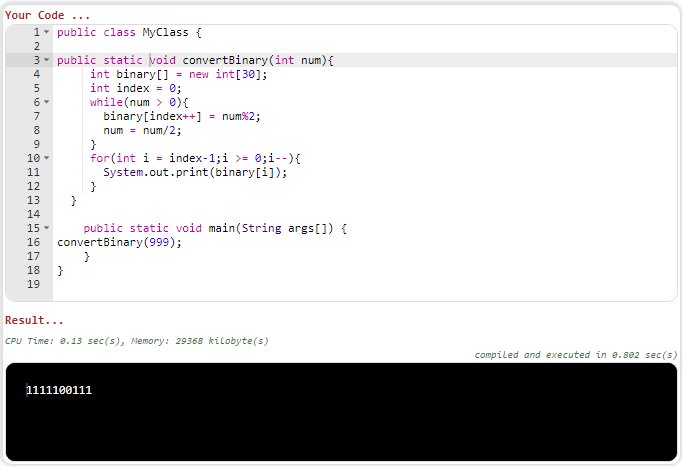
Мы просто делим на два до тех пор, пока число не кончится. Например для числа 999 наш методы выведет следующее: