Арифметика рациональных чисел на C#

Стандартная арифметика использует целые числа или значения с плавающей запятой для операндов и результатов. Рациональные числа, или дроби, не относятся к стандартным типам данных. В этой статье мы создадим структуру для дробей и добавим арифметические функции.

Рациональные числа

Рациональное число - это значение, которое может быть выражено как отношение двух целых значений. Такое число можно записать в виде дроби, содержащей два целых числа, расположенных одно над другим, разделенных горизонтальной линией. Например, 3/4, 1/2 или 8/9. Эти два числа называются числителем и знаменателем; числитель находится вверху дроби, а знаменатель - внизу.

Использование рациональных чисел для арифметики имеет некоторые преимущества по сравнению с использованием десятичных значений. Главное преимущество - это точность. При десятичных значениях ошибки округления могут возникать в небольших количествах из-за способа хранения значений. Это можно увидеть в следующем примере кода. Хотя начальное значение делится, а затем умножается на одно и то же число, результат не совпадает с исходным значением. Если бы использовались рациональные числа, эта проблема округления не была бы введена.

decimal d = 1;
d /= 3;
d *= 3;
 
Console.WriteLine(d);   // "0.9999999999999999999999999999"

Создание структуры RationalNumber

В этой статье мы разработаем новую структуру для хранения рациональных чисел и управления ими. Структура RationalNumber может быть создана так же легко, как и класс. Однако в этом случае предпочтительна структура, в которой рациональные числа демонстрируют поведение типов значений, а не ссылочных типов.

Для простоты в этой статье структура RationalNumber будет создана в проекте консольного приложения. Возможно, вы захотите создать коллекцию в библиотеке классов вместо этого для использования в своих собственных проектах. Для начала создайте новое консольное приложение под названием "RationalNumberDemo". Добавьте новый файл класса в проект с именем "RationalNumber".

Новый класс кода будет содержать стандартное объявление для класса. Замените это следующим определением структуры.

struct RationalNumber
{
}

Создание свойств

Структура рационального числа требует двух свойств. Это целочисленные значения, представляющие числитель и знаменатель дроби. Каждое из них будет доступно только для чтения, так как установка этих значений будет ограничена конструктором.

Чтобы добавить свойства, добавьте в структуру следующий код:

private int _numerator;
private int _denominator;
 
public int Numerator
{
    get { return _numerator; }
}
 
public int Denominator
{
    get { return _denominator; }
}

Добавление конструктора

Один конструктор будет отвечать за установку значений числителя и знаменателя. Добавьте следующий код конструктора:

public RationalNumber(int numerator, int denominator)
{
    if (denominator == 0)
        throw new ArgumentException("The denominator must be non-zero.");
 
    if (denominator < 0)
    {
        numerator *= -1;
        denominator *= -1;
    }
 
    _numerator = numerator;
    _denominator = denominator;
 
    ReduceToLowestTerms();
}

Конструктор выполняет четыре ключевых процесса. Во-первых, знаменатель проверяется, чтобы убедиться, что он не равен нулю. Если бы был разрешен ноль, значение всей дроби всегда было бы бесконечным, и попытка оценить это значение вызвала бы исключение деления на ноль.

После проверки знаменатель проверяется, чтобы определить, является ли он отрицательным. Хотя было бы вполне приемлемо иметь отрицательный знаменатель, более обычно выражать дробь с положительным. Для достижения этой цели, если знаменатель отрицательный, и он, и этот числитель умножаются на -1. Это не меняет общего значения дроби, только ее представление.

Третий этап заключается в хранении числителя и знаменателя в полях резервного хранилища для их соответствующих свойств. После сохранения вызывается метод ReduceToLowestTerms. Этот метод описан ниже.

Сокращение дроби до ее наименьших значений

Одно рациональное число может быть выражено в виде множества различных дробей. Например, одна вторая (1/2) может быть записана с числителем два и знаменателем четыре, или как 4/8 или 5/10. Каждое из этих представлений является допустимым, но, как правило, предпочтительно показывать дробь в ее наименьших выражениях. Это означает, что числитель и знаменатель являются наименьшими числами, возможными для рационального числа.

Чтобы уменьшить дробь до ее наименьших членов, необходимо найти наибольший общий делитель (НОД) числителя и знаменателя. Это наибольшее число, на которое можно разделить обе части дроби, сохраняя при этом два целых числа. Метод ReduceToLowestTerms вызывает дополнительный метод для определения GCD и делит числитель и знаменатель на это значение.

Добавьте метод ReduceToLowestTerms в структуру:

private void ReduceToLowestTerms()
{
    int greatestCommonDivisor = RationalNumber.GetGCD(_numerator, _denominator);
    _numerator /= greatestCommonDivisor;
    _denominator /= greatestCommonDivisor;
}

Нахождение наибольшего общего делителя

Нод двух значений может быть определен с помощью евклидова алгоритма. Этот алгоритм следует итеративному процессу. Первое значение делится на второе значение и определяется остаток. Если остаток равен нулю, то НОД является первым значением. Если остаток не равен нулю, процесс повторяется с использованием второго члена и остатка от вычисления. Алгоритм и его доказательство описаны в приведенной выше ссылке.

Для реализации алгоритма добавьте следующий метод GetGCD. Метод вызывает себя итеративно до тех пор, пока не будет определен наибольший общий делитель. Поскольку он использует поля экземпляра, он может быть объявлен как статический:

private static int GetGCD(int term1, int term2)
{
    if (term2 == 0)
        return term1;
    else
        return GetGCD(term2, term1 % term2);
}

При создании нового рационального числа конструктор уменьшает его до самых маленьких значений, используя два добавленных метода. Теперь это можно проверить, используя следующий код в основном методе класса программы:

RationalNumber rn = new RationalNumber(5, 10);
Console.WriteLine("{0}/{1}", rn.Numerator, rn.Denominator);     // Выведет "1/2"

Создание оператора сложения

Теперь, когда рациональная числовая структура способна содержать дробь в ее наименьших значениях, мы можем добавить арифметические функции. Для достижения этой цели мы перегрузим операторы+, -, * и / новыми версиями, которые обеспечивают правильную функциональность для сложения, вычитания, умножения и деления дробей. Первым будет создан оператор сложения. Чтобы сложить два рациональных числа вместе, используется следующая формула:



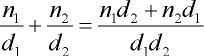
Эту формулу можно добавить в структуру, добавив следующий перегруженный оператор, который просто создает новое рациональное число, используя уравнение, показанное выше. Акт создания новой дроби также автоматически сократит ее до минимума.

public static RationalNumber operator +(RationalNumber r1, RationalNumber r2)
{
    return new RationalNumber((r1.Numerator * r2.Denominator)
        + (r2.Numerator * r1.Denominator), r1.Denominator * r2.Denominator);

Добавление оператора вычитания

Вычитание рациональных чисел использует формулу, аналогичную сложению. Это:



Чтобы создать перегруженный оператор вычитания, добавьте в структуру следующий код.

public static RationalNumber operator -(RationalNumber r1, RationalNumber r2)
{
    return new RationalNumber((r1.Numerator * r2.Denominator)
        - (r2.Numerator * r1.Denominator), r1.Denominator * r2.Denominator);
}

Добавление операторов умножения и деления

Наконец, мы можем добавить операторы для умножения и деления. Для умножения числители дроби умножаются вместе, как и знаменатели. Для деления делимая дробь инвертируется перед выполнением умножения. Формулы для этих операций следующие:



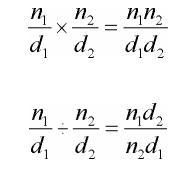
Чтобы создать два оператора, добавьте в структуру следующий код:

public static RationalNumber operator *(RationalNumber r1, RationalNumber r2)
{
    return new RationalNumber(r1.Numerator * r2.Numerator, r1.Denominator * r2.Denominator);
}
 
public static RationalNumber operator /(RationalNumber r1, RationalNumber r2)
{
    return new RationalNumber(r1.Numerator * r2.Denominator, r1.Denominator * r2.Numerator);
}

Тестирование арифметики рациональных чисел

Завершенная структура теперь может быть протестирована с помощью основного метода класса программы. Попробуйте выполнить следующие вычисления:

RationalNumber r1 = new RationalNumber(3, 5);
RationalNumber r2 = new RationalNumber(4, 7);
 
RationalNumber add = r1 + r2;   // add = 41/35
RationalNumber sub = r1 - r2;   // sub = 1/35
RationalNumber mul = r1 * r2;   // mul = 12/35
RationalNumber div = r1 / r2;   // div = 21/20