Введение в 3D графику для новичков

Мир вокруг нас трехмерен, но экран компьютера плоский (двумерный). Как же тогда можно отобразить 3D-информацию на 2D-экране? Войдите в мир 3D-графики.

Система координат

Для начала нам нужно определить, где находится точка. Для того, чтобы описать это, нам нужно определить систему координат. Простая из них называется декартовой координатой – это система, где каждая точка задается как ее расстояние от начала координат, которое само является просто определяется как точка 0. Другая система координат - сферическая система координат, в которой точка задается ее расстоянием от начала координат и два угла, описывающие его ориентацию относительно начала координат, описаны более подробно ниже.

Перед вами 2D Декартовая система координат, которая должна выглядеть знакомо каждому, кто когда-нибудь брал уроки математики:



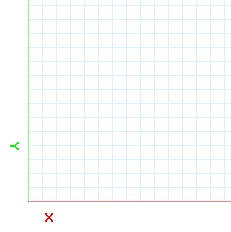
В двумерном пространстве у нас есть 2 измерения в системе координат, X и Y. в трехмерном пространстве мы имеем нужно добавить 3-й размер Z. В этом проекте оси X и Y описывают землю и ось Z описывает положение над землей.



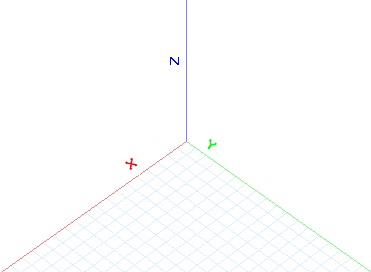
Координаты глаза (наблюдателя)

Мировые координаты представляют собой 3D координаты, которые мы пытаемся получить рисуя на экране. Для того, чтобы сделать это, необходимо сначала определить точку зрения, обычно называемую "глазом". Тогда координаты мира должны быть указаны таким образом, что начало координат находится на глазе, оси X и Y параллельны экрану, и ось Z указывает наружу перпендикулярно к экрану.

Мы также должны ввести понятие сферических координат - система координат где точка описывается ее расстоянием от начала координат, ρ (произносится как "Ро"), и его ориентация задается 2 углами, θ и φ (тета и phi).

Для преобразования координат экрана в координаты глаз необходимо выполнить следующие действия:

• Переместите начало координат из точки начала координат мира (0, 0, 0) в точку начала координат глаза, описанную выше. координаты: (Xe, Ye, Ze) . Расстояние, которое перемещается, представлено ρ, и мы можем пишите (Xe, Ye, Ze) = (ρ*sin (φ) * cos (θ), ρ * sin (φ)*sin (θ), ρ*cos(θ)) в сферических координатах.
• Поверните систему координат вокруг оси Z на заданную величину, в в данном случае угол θ. Это позволит установить расположение глаза по горизонтали на экран; при изменении значения θ, представьте себя на земле, хождение вокруг объекта.
• Поверните систему координат вокруг оси X на угол φ. Это позволит установить расположение глаза вертикально на экране; по мере изменения этого значения, представьте себе, что вы смотрите на объект в центре с разных позиций, как вы поднимаетесь и спускаетесь по лестнице.

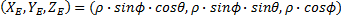Теперь у нас есть очки (xw, yw, zw), описывающие мировые координаты каждой точки в объекте (это независимая переменная.) У нас также есть постоянная точка описывающая то, где находится глаз на экране (как в декартовых, так и в сферических координатах). Нам также даны углы θ и ρ, описывающие два поворота, необходимые для размещения объектов на экране, рассматриваемых из любого положения, которое мы хотим. Самый простой способ описать эти уравнения-через "матрицу просмотра" V, такую что





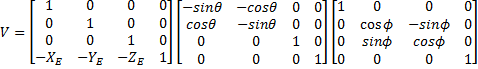
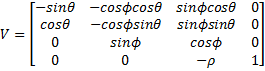
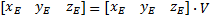
Обратите внимание, что каждая матрица соответствует каждому шагу в контуре выше, и матрицы умножаются друг на друга, чтобы объединить в a одиночное преобразование. Также отметим, что ρ получается с помощью сферической координаты представления о том, что Xe, Ye, Ze и упрощение. Этот уровень математики выходит за рамки данной статьи.

Перспектива

Можно нарисовать координаты X и Y глаз непосредственно и просто игнорировать ось Z но это вызывает проблему: объекты, которые находятся далеко, будут выглядеть так же, как и объекты, которые находятся неподалеку. В реальной жизни, чем дальше находится объект, тем меньше он выглядит. Это называется "перспектива", и может быть смоделирована путем уменьшения расстояния от точки до происхождение основано на значении Z.

Для того, чтобы описать перспективу, нам нужно учитывать расстояние от объекта до объекта управления. Если глаз находится близко к экрану, то объект будет намного больше искажен, чем если бы он был дальше. Для этого мы будем использовать переменную d. Это значение может быть произвольно установлено, либо оно может быть рассчитан на основе размера объекта и значение ρ, описанное в предыдущем разделе.

Уравнения для получения перспективного преобразования выглядят следующим образом, с помощью (X, Y) будучи точкой на экране и еще ... (x, y, z) быть точкой в координатах глаза (очерченных выше).




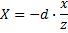
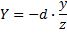
Одна дополнительная вещь, чтобы иметь в виду, что расчеты выполняются с помощью предположение, что начало экрана находится в верхнем левом углу; однако, это делает больше смысл начинать в центре экрана. Таким образом, значения X и Y выше должны будут складываться и вычитаться из координат центра; Y-координаты вычитаются, так как ось Y экрана увеличивается, когда он идет вниз, в то время как уравнения следуйте стандартным математическим соглашениям значений оси Y, уменьшающихся по мере ее уменьшения.

Применение уравнений

Для преобразования заданной 3D-точки в 2D-точку используется следующий псевдокод. Предположим, что индексация матрицы идет от 1, поэтому V[1] [1] относится к первому элементу.

Matrix worldToEye
	Given rho, theta, phi
	V[1][1] = -sin(theta)	V[1][2] = -cos(phi) * cos(theta)	V[1][3] = sin(phi) * cos(theta)
	V[2][1] = cos(theta)	V[2][2] = -cos(phi) * sin(theta)	V[2][3] = sin(phi) * sin(theta)
	V[3][1] = 0		V[3][2] = sin(phi)		V[3][3] =cos(phi)	V[3][4]=-rho
	Return V
End

Point2D worldToScreen(Point3D worldPoint)
	V = worldToEye
	xE = xW * V[1][1] + yW * V[2][1]
	yE = xW * V[2][1] + yW * V[2][2] * zW * V[3][2]
	zE = xW * V[3][1] + yW * V[2][3] * zW * V[3][3] + v[4][3]
	
	X = -d * xE / zE
	Y = -d * yE / zE

	return new Point2D(centerX + X, centerY - Y)
End

Учитывая приведенные выше уравнения, мы можем отобразить любую 3D-точку на экране. Мы также можем рисовать линии и более сложные формы между этими точками.

Выборка задних граней

В трехмерном мире объекты могут быть просмотрены с нескольких углов; в зависимости от угла, видны различные части объекта. Если мы пытаемся сделать плоский квадрат с красным фронтом и синей задней частью, нам нужно знать, в какую сторону объект обращен относительно к глазу, чтобы определить, какой цвет использовать, чтобы заполнить его.

Здесь можно использовать простую технику, известную как обратный отбор. Он основан исходя из принципа, что если объект рассматривать со спины, то ориентация объекта на заднем плане не зависит от его положения. точки, определяющие его, перевернуты. Попробуйте нарисовать фигуру, как тот, что ниже на куске затем переверните его перед вашим экраном; вы увидите, что я имею в виду.



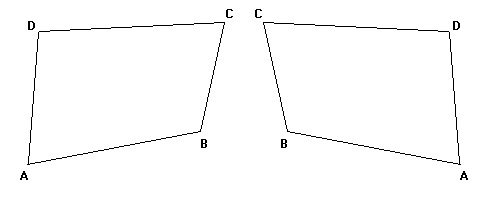
Обратите внимание, что следование последовательности A, B, C, D на первом рисунке приводит к a движение против часовой стрелки, при этом следуя той же последовательности На втором рисунке (который на самом деле является первым изображением, рассматриваемым сзади) приводит к движению по часовой стрелке. Это будет использовано в наших интересах.

Предположим, что все 3D точки полигональной грани заданы таким образом, что когда лицо просматривается спереди, его точки должны быть против часовой стрелки. Таким образом, если точки заканчиваются по часовой стрелке во время визуализации, мы знаем, что мы просматриваем эту грань сзади. Основываясь на этих знаниях, мы знаем, какой цвет необходимо использовать для заполните многоугольник.

Set As = worldToScreen(A), Bs = worldToScreen(B), Cs = worldToScreen(C), Ds = worldToScreen(D)
If orientation(As, Bs, Cs, Ds) is counterclockwise
	Set color = frontColor
else
	Set color = backColor
end if
fillPolygon(As, Bs, Cs, Ds)

Рендеринг 3D-мира

Для того чтобы дать представление о том, где находятся вещи, часто используется система координат визуализируется на экране. Для того, чтобы сделать это, нужно просто нарисовать линию от начало координат (0,0,0) до произвольно большой точки на расстоянии D на каждом из 3 оси. Другими словами, линии рисуются от (0,0,0) до (D, 0, 0), (0, D, 0), и (0,0, D). Нет никакого официального стандарта для окраски осей, но общая мнемоника это использовать красный для X, зеленый для Y и синий для Z-так как RGB и XYZ – стандартный порядок.