Улитка Паскаля на C++ с поворотом и анимацией

Выполнена новая небольшая, но интересная программа. Текст задачи:

Разработать GUI-приложение (WinForms C++) с использованием графики и анимации. Построить кривую улитка Паскаля по заданному параметрическому представлению x = cos²t + b cos t, y = a cos t sin t + b sin t, a > 0, b > 0, t ∈ [0, 2π]



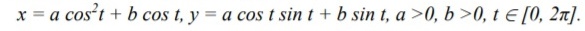
Рассмотреть случаи, когда b > 2a, a < b < 2a, a > b



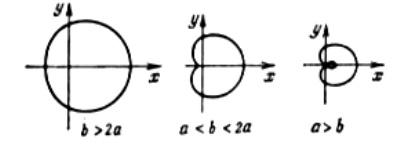
Требуется разработать приложение, которое:

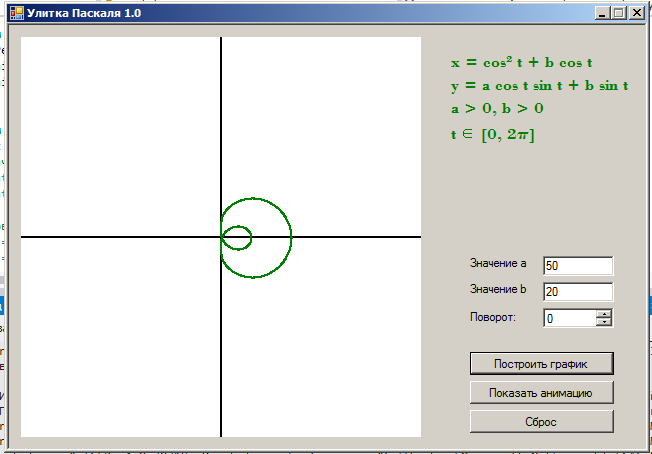
• Выводит улитку Паскаля на экран
• Позволяет изменять параметры с последующей перерисовкой
• Позволяет задавать угол поворота осей и графика функции с последующей перерисовкой
• Анимирует построение кривой

В итоге мы получим вот такое симпатичное приложение:



Немного теории по улитке Паскаля

Улитка (лимакон) Паскаля был открыт Этьеном Паскалем (отцом Блеза Паскаля) и назван другим французом Жилем-Персоном Робервалем в 1650 году, когда он использовал его в качестве примера своих методов рисования касательных, т.е. дифференцирования.

Название "лимакон" происходит от латинского limax, что означает "улитка". Этьен Паскаль переписывался с Мерсенном, чей дом был местом встреч известных геометров, включая Роберваля.

Когда b = 2ab = 2a, то лимакон становится кардиоидой, в то время как если b = ab = a, то он становится трисектрисой. Обратите внимание, что эта трисектриса не является трисектрисой Маклорена.

Улитка Паскаля это аналлагматическая кривая. Улитка также является катакаустикой круга, когда световые лучи исходят из точки на конечном (ненулевом) расстоянии от окружности. Это было показано Томасом де Сен-Лораном в 1826 году.

Ход решения на C++

Если бы у нас был обычный график функции, то есть простая зависимость y от x, то мы бы задали интервал x (например от -100 до 100), вычислили все значения y на данном интервале, получили 200 точек и эти точки отобразили бы на плоскости.

Но тут у нас параметрическое представление, что делает задачу несколько более сложной. Впрочем, не очень. Мы просто берем и проходим как бы по кругу из 360 градусов (шагов) - t ∈ [0, 2π]

for (int i = 0; i <= 360; i++){
	double f = i * PI / 180;
	m_x[i] = a * Math::Cos(f)* Math::Cos(f) + b* Math::Cos(f);
	m_y[i] = a * Math::Cos(f)* Math::Sin(f) + b* Math::Sin(f);

А затем рисуем их

//рисуем график по точкам
for (int j=0; j<360; j++){
	//начальные точки графика
	Point pt1 = Point(m_x[j] + 200, m_y[j] + 200);
	Point pt2 = Point(m_x[j] + 200, 0 - m_y[j] + 200);

	//поворот
	pt1 = getRotatePoint(angleRotation, pCenter, pt1);
	pt2 = getRotatePoint(angleRotation, pCenter, pt2);

	e->Graphics->FillRectangle(System::Drawing::Pens::Green->Brush, pt1.X, pt1.Y, 2, 2);//одно значение y
	e->Graphics->FillRectangle(System::Drawing::Pens::Green->Brush, pt2.X, pt2.Y, 2, 2);// второе значение y
}

Поворот

При этом не забывая использовать метод поворота на необходимое число градусов

Point getRotatePoint(int angle, PointF pCenter, PointF pTarget) {
	double angleRadian = angle * PI / 180; //переводим угол в радианты

	float x = (float)((pTarget.X - pCenter.X)*Math::Cos(angleRadian) - (pTarget.Y - pCenter.Y) * Math::Sin(angleRadian) + pCenter.X);
	float y = (float)((pTarget.X - pCenter.X)*Math::Sin(angleRadian) + (pTarget.Y - pCenter.Y) * Math::Cos(angleRadian) + pCenter.Y);

	Point pEnd = Point(x, y);
	return pEnd;
}

Обработка ошибок

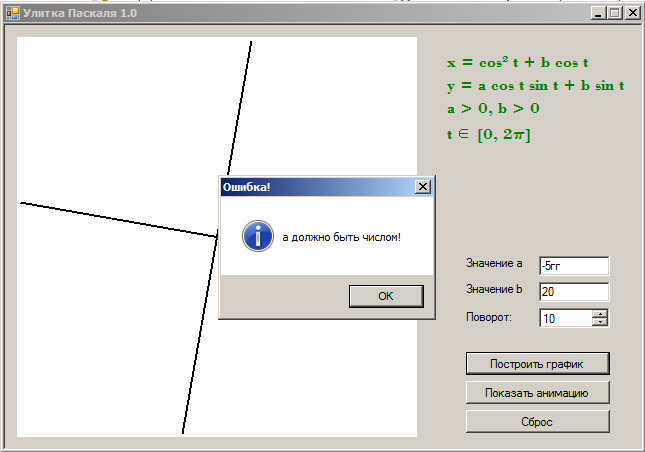
Не забудем поставить и защиту от ввода некорректных значений. Вот одно из условий нашей программы:

try {
	a = Convert::ToDouble(textBox1->Text);
}
catch (FormatException^ ex) {
	MessageBox::Show("a должно быть числом!", "Ошибка!", MessageBoxButtons::OK, MessageBoxIcon::Asterisk);
	return 1;
}

Анимация

Анимация достигается тем, что процесс прорисовки каждой точки происходит с определенной задержкой. Также не забываем использовать элемент backgroundWorker – чтобы считать и обновлять график функции в фоне, чтобы не происходило зависания интерфейса GUI программы.

В настоящий момент цена полных исходников программы с комментариями в коде составляет 500 рублей.
заметки, си плюс плюс, графики, функции, программы